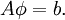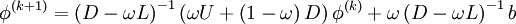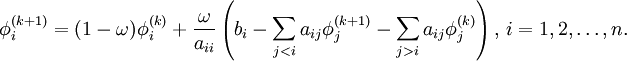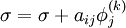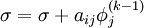Successive over-relaxation method - SOR
From CFD-Wiki
m (Successive over-relaxation method moved to Successive over-relaxation method - SOR) |
|||
| (2 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | == Introduction == | |
| - | + | We seek the solution to set of linear equations <br> | |
| - | + | :<math> A \phi = b. </math> <br> | |
| - | + | ||
| - | <math> | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | In matrix terms, the successive over-relaxation (SOR) iteration can be expressed as | |
| - | === | + | :<math> |
| - | --- | + | \phi^{(k+1)} = \left( {D - \omega L} \right)^{ - 1} \left( {\omega U + \left( {1 - \omega } \right)D} \right)\phi^{(k)} + \omega \left( {D - \omega L} \right)^{ - 1} b |
| - | + | </math> | |
| - | : for k := 1 step 1 | + | |
| + | where <math>D</math>, <math>L</math>, and <math>U</math> represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix <math>A</math>, <math>k</math> is the iteration count, and <math> \omega </math> is a relaxation factor. This matrix expression is not usually used to program the method, and an element-based expression is used: | ||
| + | |||
| + | :<math> | ||
| + | \phi^{(k+1)}_i = (1-\omega)\phi^{(k)}_i+\frac{\omega}{a_{ii}} \left(b_i - \sum_{j<i}a_{ij}\phi^{(k+1)}_j-\sum_{j>i}a_{ij}\phi^{(k)}_j\right),\, i=1,2,\ldots,n. | ||
| + | </math> | ||
| + | |||
| + | Note that for <math>\omega = 1</math> that the iteration reduces to the [[Gauss-Seidel method| Gauss-Seidel]] iteration. As with the [[Gauss-Seidel method]], the computation may be done in place, and the iteration is continued until the changes made by an iteration are below some tolerance. | ||
| + | |||
| + | The choice of relaxation factor is not necessarily easy, and depends upon the properties of the coefficient matrix. For symmetric, positive definite matrices it can be proven that <math>0<\omega<2</math> will lead to convergence, but we are generally interested in faster convergence rather than just convergence. | ||
| + | |||
| + | == Algorithm == | ||
| + | Chose an initial guess <math>\phi^{0}</math> to the solution <br> | ||
| + | : for k := 1 step 1 until convergence do <br> | ||
:: for i := 1 step until n do <br> | :: for i := 1 step until n do <br> | ||
::: <math> \sigma = 0 </math> <br> | ::: <math> \sigma = 0 </math> <br> | ||
::: for j := 1 step until i-1 do <br> | ::: for j := 1 step until i-1 do <br> | ||
| - | :::: <math> \sigma = \sigma + a_{ij} | + | :::: <math> \sigma = \sigma + a_{ij} \phi_j^{(k)} </math> |
::: end (j-loop) <br> | ::: end (j-loop) <br> | ||
::: for j := i+1 step until n do <br> | ::: for j := i+1 step until n do <br> | ||
| - | :::: <math> \sigma = \sigma + a_{ij} | + | :::: <math> \sigma = \sigma + a_{ij} \phi_j^{(k-1)} </math> |
::: end (j-loop) <br> | ::: end (j-loop) <br> | ||
| - | ::: <math> \sigma = {{\left( { | + | ::: <math> \sigma = {{\left( {b_i - \sigma } \right)} \over {a_{ii} }} </math> |
| - | ::: <math> | + | ::: <math> \phi_i^{(k)} = \phi_i^{(k - 1)} + \omega \left( {\sigma - \phi_i^{k - 1} } \right) </math> |
:: end (i-loop) | :: end (i-loop) | ||
:: check if convergence is reached | :: check if convergence is reached | ||
: end (k-loop) | : end (k-loop) | ||
| - | |||
| - | |||
| - | - | + | ''TODO - add references, more about relaxation factor'' |
| - | + | ||
Latest revision as of 02:08, 19 December 2005
Introduction
We seek the solution to set of linear equations
In matrix terms, the successive over-relaxation (SOR) iteration can be expressed as
where 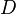 ,
, 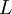 , and
, and 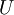 represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix
represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix 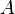 ,
,  is the iteration count, and
is the iteration count, and 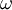 is a relaxation factor. This matrix expression is not usually used to program the method, and an element-based expression is used:
is a relaxation factor. This matrix expression is not usually used to program the method, and an element-based expression is used:
Note that for 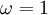 that the iteration reduces to the Gauss-Seidel iteration. As with the Gauss-Seidel method, the computation may be done in place, and the iteration is continued until the changes made by an iteration are below some tolerance.
that the iteration reduces to the Gauss-Seidel iteration. As with the Gauss-Seidel method, the computation may be done in place, and the iteration is continued until the changes made by an iteration are below some tolerance.
The choice of relaxation factor is not necessarily easy, and depends upon the properties of the coefficient matrix. For symmetric, positive definite matrices it can be proven that 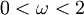 will lead to convergence, but we are generally interested in faster convergence rather than just convergence.
will lead to convergence, but we are generally interested in faster convergence rather than just convergence.
Algorithm
Chose an initial guess 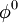 to the solution
to the solution
- for k := 1 step 1 until convergence do
- for i := 1 step until n do
-
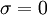
- for j := 1 step until i-1 do
-
- end (j-loop)
- for j := i+1 step until n do
-
- end (j-loop)
-
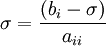
-
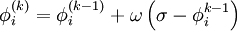
-
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (k-loop)
TODO - add references, more about relaxation factor