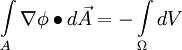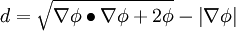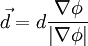Transport equation based wall distance calculation
From CFD-Wiki
| (One intermediate revision not shown) | |||
| Line 18: | Line 18: | ||
Where as the wall distance vector could be written as: <br> | Where as the wall distance vector could be written as: <br> | ||
:<math>\vec d = d{{\nabla \phi } \over {\left| {\nabla \phi } \right|}} </math> | :<math>\vec d = d{{\nabla \phi } \over {\left| {\nabla \phi } \right|}} </math> | ||
| + | |||
| + | The foregoing method for evaluation of wall distances was proposed by D.B.Spalding [1994], mainly for the purpose of calculating, for arbitrary complex geometries, the wall distances required by various low-Reynolds-number turbulence closure models. Spalding's proposal was mainly intuitive, but the method has been described in a formal mathematical framework by Fares & Schroder (2002). | ||
| + | |||
| + | D.B.Spalding, ‘Calculation of turbulent heat transfer in cluttered spaces’, Proc. 10th Int. Heat Transfer Conference, Brighton, UK, (1994). | ||
| + | |||
| + | E.Fares & W.Schroder, ‘Differential Equation for Approximate Wall Distance' Int.J.Numer.Meth., 39:743-762, (2002). | ||
| + | ---- | ||
| + | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Latest revision as of 12:31, 2 August 2006
Wall-distance variable
Wall distance are required for the implementation of various turbulence models.
The approaximate values of wall distance could be obtained by solving a transport equation for a variable called wall-distance variable or 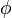 .
.
The transport equation for the wall distance variable could be written as:
with the boundary conditions of Dirichlet at the walls as 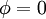 and Neumann at other boundaries as
and Neumann at other boundaries as 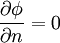
This transport equation could be solved with any of the approaches similar to that of Poisson's equation.
Wall distance calculation
Wall distance from the solution of this transport equation could be easily obtained as:
Where as the wall distance vector could be written as:
The foregoing method for evaluation of wall distances was proposed by D.B.Spalding [1994], mainly for the purpose of calculating, for arbitrary complex geometries, the wall distances required by various low-Reynolds-number turbulence closure models. Spalding's proposal was mainly intuitive, but the method has been described in a formal mathematical framework by Fares & Schroder (2002).
D.B.Spalding, ‘Calculation of turbulent heat transfer in cluttered spaces’, Proc. 10th Int. Heat Transfer Conference, Brighton, UK, (1994).
E.Fares & W.Schroder, ‘Differential Equation for Approximate Wall Distance' Int.J.Numer.Meth., 39:743-762, (2002).
Return to Numerical Methods