User talk:Tsaad
From CFD-Wiki
Tony:
My name is Gordan Feric and I provided e-Solutions for Energy Conversion Systems material.
How come it is not related to CFD Online?
Thanks,
Gordan
Hi Tony,
I don't know if this should be on my talk page or yours, so I'll put it here. While I agree that there should be consistency across the pages, I don't agree with using all capitals - especially since it is not consistent with linear algebra texts and literature. We should strike a balance there, and in many of the texts/papers I have, Ax=b is used for linear systems, not A\phi=b (or any capitalization variation thereof). There is a difference between solvers appropriate for A\vec{x}=\vec{b} and solvers appropriate for AX=B (all matrices). We muddy the water on that issue if we use all capitals all the time. Thus, I disagree that using \Phi will be clearer.
In the interests of compromise, I suggest the following: use upper case for matrices, denote vectors with \vec, and use lower case (with subscripts) for elements of either. I was in the process of editing the LU page, and that is what I have done with that (except for the elements of L and U, which I'll fix after I get done with my grading). I think it looks pretty good.
(Two side notes: The only reason there was still a "B" in the GE page was that you saved an edit while I was in process of doing my edit. When I merged my edits back in, I missed that. Also, I don't think that using "A \cdot b" for matrix-vector multiplication is a good idea)
Regards, Jason
Vector Nomenclature
Hi Tony,
I can give several reasons why I prefer x to 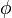 : First, it is the one that I see most in the linear algebra literature, so it is easier to proofread algorithms, etc. Second, in my opinion it looks better. When more than one vector is involved, it is better to have them be all roman letters (see LU decomposition method) rather than one roman, another greek, etc. Third (and most importantly), it is usual to use greek letters for scalar multipliers (see the Conjugate gradient methods). If greek letters are getting used for both scalars and vectors, I think that only makes confusion more likely.
: First, it is the one that I see most in the linear algebra literature, so it is easier to proofread algorithms, etc. Second, in my opinion it looks better. When more than one vector is involved, it is better to have them be all roman letters (see LU decomposition method) rather than one roman, another greek, etc. Third (and most importantly), it is usual to use greek letters for scalar multipliers (see the Conjugate gradient methods). If greek letters are getting used for both scalars and vectors, I think that only makes confusion more likely.
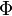 and
and 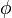 are not free of alternate meanings (e.g. viscous dissipation and potential function), and the nomenclature collision problem is essentially unavoidable no matter what is chosen.
are not free of alternate meanings (e.g. viscous dissipation and potential function), and the nomenclature collision problem is essentially unavoidable no matter what is chosen.
Regards,
Jason
