 |
|
|
[Sponsors] | |||||
How to obtain turbulent kinetic energy data from LES model of Ansys CFX? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
Results files are obtained after simulating Stirred tank reactor and i would like to know the predictions of turbulence kinetic energy of the LES Smagorinsky model in the Ansys CFX 11. I can't find a procedure as LES doesn't directly calculate the kinetic energy. Please let me know if someone has an idea. Thanks
|
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
You need to define the turbulence kinetic energy as a function of the velocity somehow. You can take time or space (or both!) averages of the velocity fields and use that to determine the averaged and fluctuating components. From the fluctuating component you can get k.
I discuss this in my PhD thesis, in the chapter where I look at the square piston engine (chapter 6 I think) - http://hdl.handle.net/2100/248 |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
I agree with you.I have found in the literature a correlation which states turbulence kinetic energy as a function of the velocity as shown below
k 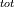 =k =k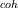 +k +k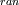 =1/2*( =1/2*(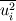 - -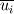 ^2) ^2)here u represents the velocity, i represents repeted index. I don't understant the difference between 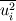 and and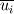 ^2 ^2I have even got time average of velocity fields. but i dont know (or i can't find out) how to use that to determine the averaged and fluctuating component. Can you help with this. Thanks Last edited by rsin; September 21, 2009 at 21:38. |
|
|
|

|
|
|
|
|
#4 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
Sounds like you need to read a text book about Reynolds and Fauve averaging. It is covered by any fluid mechanics textbook which develops the basics of turbulence modelling. In fact the CFX documentation even has a basic description of it, but a good textbook will introduce it to beginners better.
But to directly answer your question - if you have calculated the average velocity field then you simply need to calculate the average of the square of the velocity and then some simple post-processing in CFD-Post and you are done. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
after lot of serach, a very easy method was found through CFX help files.
they state that turbulent kinetic energy for LES = 1/2 * (Velocity.Trnrms^2 -Velocity.Trnavg^2) or = 1/2 * (statistics reynolds stresses uu + ...vv + ....ww) statistical reynolds stresses are automatically calculated for the LES/SAS-SST and DES models. While .Trnrms and .Trnavg files are transient result files that have to be turned on in the output section. Just to save you a whole lot of time. 
Last edited by rsin; July 15, 2010 at 03:20. Reason: put the formula´s in the wrong place |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Lance
Join Date: Mar 2009
Posts: 669
Rep Power: 22  |
Quote:
|
||
|
|

|
||
|
|
|
#7 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
In order to find the energy dissipation rate, it is essential to understand the way in which kinetic energy is transferred between the filtered velocity field and the residual motions. The filtered kinetic energy Average of E (x,t) is obtained by filtering the kinetic energy field E (x,t) = 1/2 * average of (U * U)
or Average of E = 1/2 * average of (U * U) (1) It can be further decomposed as: Average of E = Ef + kr (2) Where Ef, the kinetic energy of the filtered velocity field, and kr the residual kinetic energy, are given by Ef = 1/2 * average of (U ) * average of ( U)(3) kr = 1/2 * Average of (U * U) - Average of (U) * average of (U) = 1/2*tauiiR(4) The conservation equation for Ef is: DEf/Dt – delta/deltaxi [ average of Uj ( 2 * mu * average of Sij – tauijr - average of p/ ro * deltaij)] = - εf - Pr(5) where epsilonf and Pr are defined as epsilonf = 2 * mu * average of Sij * average of Sij(6) Pr = - tauijr * average of Sij(7) where average of Sij is the filtered rate of strain and tauijr is the anisotropic residual-stress tensor and defined as: tauijr = tauijR - 2/3 * kr * deltaij(8) where deltaij , the kronecker delta, and tauijR, the residual –stress tensor, are defined as: deltaij= 1 when i = j and =0 when i is not equal to j(9) tauijR = Average of (Ui * Uj) - Average of (Ui) * average of (Uj)(10) In Equation 5, terms of the left hand side represents the transport and the ones on the right hand side represents the sink terms. The first sink term – εf corresponds to the viscous dissipation directly from the filtered velocity, and at high Reynolds number with filter width much larger than the Kolmogorov scale, this term is relatively small. The second sink term - Pr, which appears as a source term ( + Pr) in the equation for kr, is the rate of production of residual kinetic energy in the equation of Ef; therefore, it represents the rate of transfer of energy from the filtered motion to the residual motions. Sometimes, it is referred as the sub-grid scale (SGS) dissipation and denoted by εs. At high Reynolds number the filtered velocity field accounts for nearly all of the kinetic energy: average of E is practially to E (11) As seen above, the dominant sink for average of E is Pr, whereas that in the equation for E for two-equation models is the rate of dissipation of kinetic energy, ε; consequently: Pr is practically equal to ε (12) Hence, ε is practically equal to Pr = - tauijr * average of Sij (13) Now, both terms average of Sij and tauijr can be obtained directly from the transient results file and they need to be averaged with time. There are two different kinds of energy dissipation rates: solved and SGS. Solved, which is comparatively much smaller and can be neglected, is represented by the term εf, and SGS is represented by Pr, which is the dominant term and accounts for nearly all of the energy dissipation. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Lance
Join Date: Mar 2009
Posts: 669
Rep Power: 22  |
well, that's straight out of Turbulent Flows by Pope, right?
My question was if there's a way to estimate the contribution to k from the sub-grid model. |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
Hello Lance,
Yes, the equations are st out of the book by Pope and it helped me in understanding how and why k for LES = 1/2 * (Velocity.Trnrms^2 -Velocity.Trnavg^2) or = 1/2 * (statistics reynolds stresses uu + ...vv + ....ww) This is what i understand when i compare the equation 4 with these equations. If you think this is wrong then please do share the point of view which led you to that belief. If you find another way of calculationg k and epsilon, then plese do share it. Thanks & Regards |
|
|
|

|
|
|
|
|
#10 | |
|
Member
Peter
Join Date: Nov 2011
Posts: 46
Rep Power: 14  |
Quote:
|
||
|
|

|
||
|
|
|
#11 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
"By "average of", did you mean "filtered"?"
By average of i meant average or mean. If you have access to the data at each time-setp, then you can do a average by yourself.. it should be easy. In Fluent for LES and DNS, there is access to the twelve gradients, so you can estimate epsilon directly by doing a ensemble average of these gradients and then summing them up as shown by Sharp and Adrian (2001) PIV Study of Small-Scale Flow Structure around a Rushton Turbine. Although, if mesh is not equivalent o Kolmogorv, DNS will be underpredicting because of unavailbility of the smallest scales while for LES, a sgs models data is available which you can estimae for the unfiltered part. Cheers |
|
|
|

|
|
|
|
|
#12 | |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
There is a second direct method with which there are no arguments.
Create a 2D plane (2d plane instead of 3d to reduce amount of data and offcourse size of the files) in your geometry and extract data for each time-step in that plane. choose the three velocity components, the three directions and any other parameters that you wish. Now, i extracted these parameters in the *.txt files and then used matlab to create matrices for each parameter. This way you will have instantaneous velocity profiles at each time-step. averaging over the whole time-step will give you the mean velocity flow profiles.. Then substracting the mean from each instantenous profile will give you the fluctuating component at each time-step. estimate the square of each component and then accordingly, you will have instantanous turbulence kinetic energy at each time-step. estimate the mean of TKE over the whole time-step to find the mean TKE. Its very easy to do all of this in matlab. If need be, i can help you with matlab code.. Quote:
|
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
|
Hi colleagues,
I am working with the burger equation in 1D (DNS). Mr. Rsin, from your explanation I conclude that your implemented an ensemble average rather than a time averaged; Am I right? Is it possible to do the computation during the time marching and not as a post - processing analysis. However, what I can predict (maybe I am wrong) is that at the very first march (t=1) when you divide the velocity by dt, the value will be very big and the computation can blow up. Let me share my script for the fluctuating computation. SUBROUTINE FLUCTUATING(t) integer:: t_inner do i = 2, imax - 1 !Computing the time averaged of the velocity umean = 0 do t_inner = 1, t umean (i) = umean (i) + u(i,t_inner) end do ufluct(i,t) = u(i,t) - umean(i)/(t*dt) kap(i,t) = 0.5*ufluct(i,t)**2 end do Does it make sense??? What are your feedbacks? Also, I have read the reply from Mr. Horrocks but I got lost when he mentioned about averaging in time and space. |
|
|
|

|
|
|
|
|
#14 |
|
New Member
Join Date: Sep 2009
Posts: 20
Rep Power: 16  |
Dear Julio,
I have not worked with subroutines, so can´t tell if there is something wrong or not or give any advice. It seems to me that you are using it to estimate the mean and flucting velocity and hence the k. I can say if you create a variable you need, you could get the overall mean at the end. Still, post processing will be required to retrive that variable, plot etc. Secondly activate this varible only when your simulation has stablized or reached a certain convergence criteria.. They way your computation should not blow up.. Secondly, if you take a variable at a particular location at each time step and average it over the course of say 5000 time-steps.. what do you call that- time averaged or ensemble average?? |
|
|
|

|
|
|
|
|
#15 | |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
Quote:
Note that I said you can average in space OR time OR both. Averaging in both is unusual however. I don't know if that helps at all. |
||
|
|

|
||
|
|
|
#16 |
|
Senior Member
|
Dear Rsin thanks for your reply. I really appreciate your time and thoughts. The same to Mr. Horrocks, I am very glad you replied too.
@Rsin, In order to be strict with the definition, computing the mean from the 5000 time-steps solution, this is ensemble average because is u(i,t=1:Tsteps)/Tsteps. If we want the time averaged then it will be u(i,t=1:Tsteps)/(dt*Tsteps). Yet, will this procedure make a difference? I think it will. However, I do not have clear if the appropiate approach is ensemble or time. Wilcox uses the time averaged definition, but Pope defines the turbulent kinetic energy as the mean or expectation, in other words the mean as an ensemble average. Also, I have another doubt, this is more about concepts. You said that I need to activate this variable only when the simulation has stabilized. Aside the time averaged definition, what is the other reason?. I have seen papers with statistics starting from t=0. What if I compute the average and fluctuations from t=0 to the end? @Mr. Horrocks, your help is always important and full of insight. I remember another post where you addressed the differences between the ensemble and time average. So, if I want to be strict with the definitions, what averaged should I use. I am doing DNS of the Burger equation with forces and without force. Without the force, the initial condition results in a velocity field that is constant for all time and space. Moreover, any perturbation of that field decay toward zero. Hence, the other case with force will help me to have a high-intensity fluctuation. So, I want to compare both cases because under a LES formulation. Both cases will have different time - history solution. So, I think that I might do the statistivs (turbulent kinetic energy, dissipation of the turbulent kinetic energy, mean, fluctuation, u'rms and so forth) using the whole dataset. Am I right? most of these questions are due to my lack of experience on LES and DNS. what do you recommend me. Thanks to you all!!! Respectfully JM |
|
|
|

|
|
|
|
|
#17 | |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
Quote:
Is your flow or forcing function periodic? |
||
|
|

|
||
|
|
|
#18 |
|
Senior Member
|
Mr. Horrocks, maybe I should have started saying htat I am not using CFX. I am writing my own code for DNS of the Burger equation (1D). Thus, I will do numeric computation of the Burger equation with and without force. In other words, two different cases.
My issue is with the case without forces. Thus the initial condition will be dissipated by the viscous forces. thus, the process is non-stationary according to Wilcox book. How should I compute the statistics with this case, if the mean is not constant in time (non-stationary). My boundary condition is periodic, so I do not have anyhing that introduces perturbation into the fluid flow. |
|
|
|

|
|
|
|
|
#19 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
I am aware you are doing your own coding.
A question: How are you going to model DNS using the 1D Burger equation? DNS is inherently 3D transient. I take it from your final sentence that your flow is periodic, or at least the boundary conditions are. Then you have a few options to do the averaging functions: 1) Ensemble average where you run over many full cycles, and then take the results at the same point of the cycle averaged over your simulation. If you are in a position to run many cycles this is usually the best way of doing the averaging as it does not require assumptions of time or length scales - just that the average flow is periodic. 2) Time filtering: where you look at a variable (say velocity) at a point in your domain over time and apply a low pass filter to it. You then assume the low pass filtered result is your mean flow field and the high frequency stuff is the turbulence. 3) Space filtering: where you look at a variable (say velocity) at a certain time in your domain and apply a low pass filter to it. You then assume the low pass filtered result is your mean flow field and the high frequency stuff is the turbulence. Options 2 and 3 require assumptions about time and length scales and that can be problematic. |
|
|
|

|
|
|
|
|
#20 | |
|
New Member
|
This post in the ANSYS Student Community was helpful:
https://studentcommunity.ansys.com/t...inetic-energy/ Quote:
Last edited by MikeBravo; January 11, 2019 at 04:52. |
||
|
|

|
||
 |
| Tags |
| les, turbulence kinetic enregy |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| how to map resultd from cfx to ansys? | ritesh | CFX | 2 | June 1, 2011 07:52 |
| ATTENTION! Reliability problems in CFX 5.7 | Joseph | CFX | 14 | April 20, 2010 15:45 |
| what's the macro of SGS turbulent kinetic energy? | lcw | FLUENT | 1 | June 13, 2006 03:08 |
| Turbulent Kinetic Energy In LES | Cfd-Student | FLUENT | 0 | January 11, 2006 10:02 |
| FSI using CFX and ANSYS | Bi Chang | CFX | 2 | May 10, 2005 04:47 |