 |
|
|
[Sponsors] | |||||
non-linear terms in conservative or non-conservative form |
 5Likes
5Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Jun 2010
Posts: 111
Rep Power: 15  |
||
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,775
Rep Power: 71    |
yes, the discrete equations can drive to very different results (e.g. different wave propagation), as advice you must use always the conservative form!
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Jun 2010
Posts: 111
Rep Power: 15  |
Thanks very much.
On a slightly different note, if the non-lineaity was in an unsteady term for instance 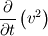 , how would one go about discretizing with respect to time? Say, Explicit Euler was being used, would it be possible to just find , how would one go about discretizing with respect to time? Say, Explicit Euler was being used, would it be possible to just find 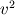 at the next time step and take the square root of that or is there more to it due to the non-linearity? I think this would reduce the accuracy but I am not really sure. at the next time step and take the square root of that or is there more to it due to the non-linearity? I think this would reduce the accuracy but I am not really sure. Thanks again! |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,775
Rep Power: 71    |
Quote:
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
cfdnewbie
Join Date: Mar 2010
Posts: 557
Rep Power: 20  |
Just as a quick addition to this: There's something called the "skew symmetric form" that avoids aliasing errors and consists of a combination of both formulations. In that sense, it might not always be advisable to use the conservative form alone, but on general, yes, use it rather than the non-con form!
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Jun 2010
Posts: 111
Rep Power: 15  |
Thanks!
Can I just ask more specifically why the conservative form is preferred. If you know any good reading material on this specific topic , please let me know. |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,775
Rep Power: 71    |
Quote:
then, many papers in journals are more specific in analyzing the properties of the conservative (divetgence) form in terms of accuracy and stability |
||
|
|

|
||
|
|
|
#8 |
|
Super Moderator
|
If solutions are discontinuous, then conservative form should be used.
For smooth solutions, the skew symmetric form can be used; it conserves energy and thats one of the reasons it is used. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| conservative, non conservative form???? | vijesh joshi | Main CFD Forum | 5 | April 21, 2022 06:37 |
| Rewriting twoPhaseEulerFoam in conservative form | alberto | OpenFOAM Running, Solving & CFD | 36 | May 27, 2016 09:06 |
| Conservative form of Navier Stokes equation. | balkrishna | OpenFOAM Running, Solving & CFD | 2 | January 25, 2012 08:33 |
| Conservative form | bardiche | Main CFD Forum | 0 | February 9, 2011 19:58 |
| solution diverges when linear upwind interpolation scheme is used | subash | OpenFOAM | 0 | May 29, 2010 01:23 |