 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Dongyue Li
Join Date: Jun 2012
Location: Beijing, China
Posts: 838
Rep Power: 17  |
Hi guys,
In physics, the Young–Laplace equation is a nonlinear partial differential equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension. But how can I deduce this equation?http://en.wikipedia.org/wiki/Young%E...place_equation 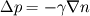 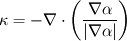
Last edited by sharonyue; June 14, 2013 at 03:06. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi, just take a differential shell element (which represents the interface between both fluids) with different radius of curvature on each side (R1 and R2). The length of the element sides are dx1 and dx2, which span a differential angle
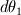 and and 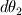 (where (where 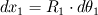 and and 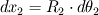 ). ).Consider static equilibrium of the shell element and you get something like this: ![\Delta p=\gamma \cdot \left[ 2\cdot dx_2 \cdot sin( d\theta_1 /2)+2\cdot dx_1 \cdot sin( d\theta_2 /2) \right] \Delta p=\gamma \cdot \left[ 2\cdot dx_2 \cdot sin( d\theta_1 /2)+2\cdot dx_1 \cdot sin( d\theta_2 /2) \right]](/Forums/vbLatex/img/af573039cd59fe893905d32338678072-1.gif) Assume small angles (sin(theta) approx. theta) and you get this: 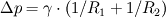 The expression comes from assuming that the pressure difference (which pushes the shell upwards normally to its surface, considering the higher pressure on the concave side of the shell) balances the forces due to surface tension, which pull the shell downwards at angles 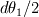 and and 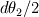 . .The easiest way is to draw the shell element with the dimensions and the force vectors and deducing the equilibrium equation. Cheers, Michujo. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Dongyue Li
Join Date: Jun 2012
Location: Beijing, China
Posts: 838
Rep Power: 17  |
Quote:
Thanks alot, after draw the shell element, I know 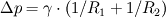 , but how can I turn it to , but how can I turn it to 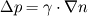 ? ?Now I only know 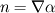 Could it be said that 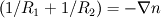 ? ?
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi, follow the variation of the normal vector along the element. Imagine that, at the center of the shell element, the normal is point upwards but, if you move along one side in the, let's say, the x direction, the normal at the edge of the element will be crooked because of the curvature of the element.
At the edge the normal will not be pointing exactly upwards but somewhat along the x direction. How much is "somewhat"? => 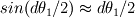 . The variation in the x coordinate is dx/2 (half length of the element along the x coordinate). . The variation in the x coordinate is dx/2 (half length of the element along the x coordinate).Therefore the variation of the x component of the normal vector as we move along the x coordinate is: 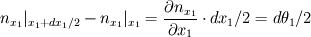 and re-arranging: and re-arranging: 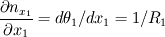 Thus 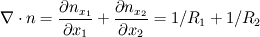 expresses the variation of the normal components due to curvature of the fluids interface. expresses the variation of the normal components due to curvature of the fluids interface.It's just some geometry and some algebraic manipulations. Cheers, Michujo. Last edited by michujo; June 14, 2013 at 09:00. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Dongyue Li
Join Date: Jun 2012
Location: Beijing, China
Posts: 838
Rep Power: 17  |
Quote:
I just came back. Thats beautiful!! I need time to see it deeply, Thanks very much Michujo!!! |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
No worries. I drew it so it's much easier to see instead of talking about vectors and differentials...
Cheers, Michujo. |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Dongyue Li
Join Date: Jun 2012
Location: Beijing, China
Posts: 838
Rep Power: 17  |
Quote:
I just think about it deeply, Thats more clear now. Thats very kool. But there is only one thing left now: I dont understand why the increment in x-component of the normal vector equals 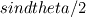 , could you explain it for a little bit? Thanks for your patience!!Or you can recommend me some papers about this. , could you explain it for a little bit? Thanks for your patience!!Or you can recommend me some papers about this.In this image, q's magnitude equals 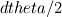 ? ?
|
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi, yes, in the image the magnitude of q is
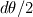 . .It's all geometry: 1) The interface element spans 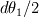 and and 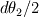 along the x1 and x2 coordinates. along the x1 and x2 coordinates.2) Also, you know that the modulus of the normal vector is 1. 3) Finally, as the normal vector is always perpendicular to the interface, by geometry, as the element turns and angle of 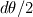 so will the normal vector. Therefore the components of the normal vector will be so will the normal vector. Therefore the components of the normal vector will be 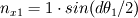 and and 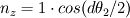 . For that you have moved a distance dx1/2 from the center of the element. . For that you have moved a distance dx1/2 from the center of the element.4) 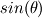 tends to tends to 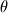 as as 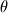 tends to zero. tends to zero.I cannot think of any reference now but I'm sure there must be tons of information out there somewhere. Cheers, Michujo. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Dongyue Li
Join Date: Jun 2012
Location: Beijing, China
Posts: 838
Rep Power: 17  |
Quote:
Cheers! |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 05:21 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 06:27 |
| error message | cuteapathy | CFX | 14 | March 20, 2012 06:45 |
| Constant velocity of the material | Sas | CFX | 15 | July 13, 2010 08:56 |
| Laplacian operator and nuSgs for heat equation | Bedotto | OpenFOAM Programming & Development | 4 | September 7, 2009 15:08 |