 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Иван Сташко
Join Date: Dec 2013
Posts: 28
Rep Power: 12  |
I have some significant experience with COMSOL. COMSOL is FEM-based. After it has solved a problem using a gross mesh, I can ask for a field value at a given point. This is not a problem and is performed using the basis functions chosen for that particular element.
I am working with some colleagues who are using two different CFD packages. Both of them tell me, that using their packages, they can only evaluate the solution at the centroids. Evaluation elsewhere is not done by interpolation, but by some kind of filtering function which actually does not really represent the solution. What are your thoughts on this matter? It seems rather odd, coming from the FEM world. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
Spectral methods are based on global interpolation by trigonometric basis polynomials. Therefore, any discrete method has a proper "shape function" like in FEM. |
||
|
|

|
||
|
|
|
#3 |
|
New Member
Иван Сташко
Join Date: Dec 2013
Posts: 28
Rep Power: 12  |
Yup, I read that there have to be these interpolation functions to perform the calculations at the volume boundaries... However, I am told that those two particular packages (Fluent and something else which I don't want to mention here) are unable to give you solution results at any point other than the centroid.
So the question is not whether the interpolation functions exist internally to the package for the purpose of finding the solution, but rather, whether it is possible to obtain a value at a given point which is not the centroid, from, let's say, the Fluent package. It seems ludicrous to me that this would be the case. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Speaking about fluent, consider that the value in a centroid is volume averaged and represents a constant over the finite volume at second order of accuracy.
Higher order representation of averaged values is not possible. That is somehow linked to filtered top-hat function |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Иван Сташко
Join Date: Dec 2013
Posts: 28
Rep Power: 12  |
OK, so I do see an least one advantage of using FEM methods, now... Or at least, of staying away from Fluent. Thank you for the help!
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
However, this is not a limit of fluent, it is the second order FV formulation that leads to value at the centroid be equal to the volume averaged value.
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Иван Сташко
Join Date: Dec 2013
Posts: 28
Rep Power: 12  |
OK, I understand that. But is it really true that these various FVM packages don't have post-processors to give the use a value at any other location?
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
||
|
|

|
|
|
|
|
#9 |
|
New Member
Иван Сташко
Join Date: Dec 2013
Posts: 28
Rep Power: 12  |
Interesting tip, thanks! To tell the truth, this other company is using a proprietary soft which doesn't have a manual on the web; I can hardly say if they will write a Tecplot file for me.
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
|
I don't know the other package you are referring to but, OF COURSE, Fluent can give you the value of some variable wherever you want; that is, Fluent has integrated post-processing capabilities.
Now, the question is: what do you need this value for? If you want a solver consistent value for some variable, you can't have nodal values in Fluent in the same way you can't have volume averaged values in FEM. I mean, you can only obtain volume averaged values in FVM as only nodal values in FEM, the variables the two codes solve for. Anything else requires some additional approximation. In FEM the approximation is on the local basis function; in FV it is based on the local interpolant used to compute the fluxes on the faces of the volume. If, instead, given a computed solution, you want some approximate value in a place whre it is not stored, then this is just interpolation and Fluent can do it as any other code. In this case, however, the consistency with the solver is not anymore required and you can go with any interpolant you want, just as in FEM. Going specifically to Fluent, given a certain point, you locate the cell it belongs to and do some of the following (according to your needs): - use the cell value (1st order) - use the cell value + a correction based on the local gradient, limited or not (2nd order) - split the located cell in tetrahedra. These tetrahedra have a vertex in the centroid (known value), one on the centroid of the faces (known value, because used to compute face fluxes) and on the nodes of the cell (values internally stored by Fluent and computed by an inverse weighted distance interpolation over the cells sharing the node). Locate the tetrahedra containing your point and use linear interpolation within the tetrahedra These methods are just if you want to do it by yourself via user provided subroutines (which, nonetheless are very easy to program). Otherwise, you can specify a plane, a line, an isosurface of anything, and export the values on it, which are linearly interpolated (you will not notice any jump between cells). |
|
|
|

|
|
|
|
|
#11 |
|
Super Moderator
|
The FEM solution is a "function" which you can evaluate anywhere you like. You can also compute cell average from the FE solution.
FVM gives you only cell average value. To approximate the solution at some particular point using the cell averages, you need to do some additional steps which may have nothing to do with FVM itself. |
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
On the other other hand, FVM can be formulated by means a built-in functional reconstrunction of cell-average value, for example think about ENO/WENO reconstruction or Barth's polynomial appromixation |
||
|
|

|
||
|
|
|
#13 | |
|
Senior Member
cfdnewbie
Join Date: Mar 2010
Posts: 557
Rep Power: 20  |
Quote:
FEM is a projection onto a given functional space, so it is indeed a "best" functional representation (in some norm) to the problem. This functional representation can now be evaluated at any given point on the compact support, so the nodal values (at any point in space) ARE defined by the projection. What am I missing here? Thank you! |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
Therefore, the FEM solution is in expressed in terms of averaged values like in FVM. The functional representation gives you values at any point but they referred as to a continuous representation of the averaged function. For example, consider the Burgers equation and project it along 1/|V| in a FEM manner. You see that the time derivative applies on the averaged function. If you use other shape functions, the time derivative works on a transformed velocity function Last edited by FMDenaro; December 22, 2013 at 12:58. |
||
|
|

|
||
|
|
|
#15 |
|
Senior Member
cfdnewbie
Join Date: Mar 2010
Posts: 557
Rep Power: 20  |
allright, I get what you are saying. thank you. a very interesting point! I never thought of FEM in that way!
|
|
|
|

|
|
|
|
|
#16 |
|
Senior Member
|
The view suggested by Filippo is very well explained in:
Karniadakis, Spencer: Spectral/hp Element Methods for CFD not exactly a FV oriented opinion. Instead, if i can go back to my point, what i was trying to say is that, given a functional representation (or test function in the view suggested by Filippo), you get some variables you solve for (cell-centered or nodal). Then, using the same functional representation (or something consistent with it), you compute all the remaining terms. I get your point praveen: when taking the functional representation from FEM the solution is already defined uniquely in all the remaining points by the interpolant itself while in FV you only get average values. However, in my view (and Filippo as well i think), what you in FEM consider as part of the functional representation (the fact that you can interpolate everywhere) is actually a reconstruction when considered from the FV point of view, the difference being just the test function used in a more general weighted residual method. Think about this: in FV we solve for average values but, of course, this does not mean that the real function we are solving for is actually constant in the cell volumes, it's just a representation. In the same way, if you select, say, a linear FEM method, you solve for the nodal values only, but does this mean that the actual function is piecewise linear? I don't think so. So, in FEM you use your functional representation to compute your terms; the same happens in FV where you also have to deal with a very bad representation (which, however, is actually linear). In my view, it is a second phase the one in which you use your information to compute the terms in your equation; the important thing is that you use consistent information, and this can be checked by checking the accuracy of the overall solver. According to your view, when in FV you want to go beyond 2nd order, you would be stacked (and probably 2nd order only appears fortuitous); instead, what you do is properly dealing with the representation and you can recover arbitrary accuracy (e.g., ADER, Spectral Volume methods). I guess that something similar happens in Petrov-Galerkin methods, where test functions and functional representations differ. |
|
|
|

|
|
|
|
|
#17 |
|
Super Moderator
|
Suppose you have a weak formulation
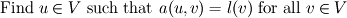 In the FEM, we approximation the function space 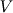 by a finite dimensional function space by a finite dimensional function space 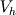 . We usually take . We usually take 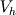 to be made of piecewise polynomials. to be made of piecewise polynomials. The FEM is 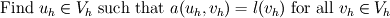 The solution 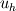 is a function which is completely determined by the FEM. is a function which is completely determined by the FEM.To represent 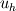 you may use a nodal basis or a modal basis, but they represent the same function. you may use a nodal basis or a modal basis, but they represent the same function.Now once 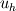 is found you can take averages of that. But you lose information in that process. If you only have cell averages, there is no unique way to get back the original function. is found you can take averages of that. But you lose information in that process. If you only have cell averages, there is no unique way to get back the original function.The Discontinuous Galerkin method is essentially a finite element method and is a higher order version of the finite volume method. In DGFEM the solution is a piecewise polynomial which is completely determined by the scheme. In this approach you obtain a function unlike in FVM. |
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
yes, the above description is general and is correct... but just try to apply the FEM to du/dt + d/dx(u^2/2-ni*du/dx) = 0 what after you project along some test function? On the other hand, in FVM the "interpolation" appears in somehow obscure way, but the functional representation of the flux function is the key to understand that shape functions are implied also in FVM. Considering the above equation in integral form (u_bar is the average function): du_bar/dt + [(u^2/2-ni*du/dx)|est - (u^2/2-ni*du/dx)|west]/h = 0 Then, the FVM implies you use a functional representation u_bar=u_bar[u]. Defined that, you can use such representation to compute everywhere the values In conclusion, my opinion is the FVM is just a special case of FEM |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
|
Dear praveen,
i still get your point and totally agree with you. But, let me ask you this: what happens if instead of v_h belonging to V_h (as for u_h), you instead use v_h as in FV (1 inside a given cell and 0 outside it)? You know better than me, integrating by parts you get the FV method. Has this, in any way, affected u_h and its functional space? I guess not. It is certainly a personal opinion, but v_h has nothing to do with u_h, it is only a mathematical tool (well, not exactly, see Mattiussi JCP 133, 289-309, 1997) Then you can think of a FV method whose solution resides in a functional space (U_h) which can be exactly the same for FEM. However, if we go back to basic 2nd order FV methods, you have that the local polynomial appears to be order 0; hence, following your line of reasoning (which is correct, i agree), we have no way to reconstruct a different polinomial in the cell and compute a different value in any point of the cell. Now, and this is probably where we disagree, what happens is that in the FV method you don't actually require u_h to be 0 outside the given cell (as you would imagine in a Galerkin approach, U_h = V_h). Hence, i can use different cell values to locally reconstruct the solution, those cell values belonging to the "element" of the given cell, which by no reason should be the same used for v_h (as happens, for example, in the Spectral Volume method... i guess). The core of the reasoning here is how you define u_h and v_h and where you use them. In FV, they are not the same, in FE Galerkin they are, in Petrov-Galerkin FE they are not. For practical convenience v_h and u_h also share the same element in FE, they do not in FV. This is possibly because, in FE, you need both u_h and v_h to compute the terms in your equations. This is not anymore the case in FV, as v_h becomes 1 and terms containing its gradient just disappears. You are thus left with u_h, which is not constrained to be defined on the same element as for v_h (the one defining the FV cell). Hence, in summary: - in FV you only need u_h to compute the terms in your equations - in FV v_h only defines the finite volume cells, not the elements over which u_h is defined, which can be almost arbitrary (see ENO/WENO) because you don't have to follow v_h - what remains in FV is the requirements that, when you want to evaluate a function in a point you use the correct element and functional space for that point; that is, those which are consistent with your discretization in the same way you do it in FEM - in a second order FV method this means that you can locate the cell where a point belongs, compute the gradient of the variable in the cell center by using the local element for the variable you are trying to interpolate and linearly interpolate from the cell center to the point trough a first order Taylor expansion. All the required information is stored in the same way it is in FEM, it is just a different information. Hope this makes sense |
|
|
|

|
|
|
|
|
#20 |
|
Super Moderator
|
Going back to the original question about evaluating solution at some arbitrary point in the domain.
Galerkin, petrov-galerkin and DGFEM all give us a function as a solution, so in this case it is very clear. You can reinterpret some Godunov FVMs as a special type of petrov-galerkin DG method for hyperbolic problems. This is done in some papers of Barth. This involves a reconstruction process and one can say to the original question that you use the reconstruction to evaluate the solution at some desired point. It may not be possible to do this in general, e.g., say for Navier-Stokes. One usually constructs schemes for inviscid and viscous terms using different ideas, and I dont think it is possible to give a proper re-intepretation as an FEM. Remember that the purpose of this re-interpretation is to give us a function that can be evaluated at a desired point. In many other FVM, the FV method itself tells you how to reconstruct the face values but may not tell you what is the reconstructed function inside the cells. In this case you have to use some reconstruction process of sufficient accuracy which may have nothing to do with the FVM. |
|
|
|

|
|
 |
| Tags |
| fvm, interpolation, numerical |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| grid dependancy | gueynard a. | Main CFD Forum | 19 | June 27, 2014 21:22 |
| Does FOAM converge to exact solution in Laplace equation? | santiagomarquezd | OpenFOAM Running, Solving & CFD | 0 | March 26, 2010 07:52 |
| Interpolation of solution in TUI | john | FLUENT | 5 | December 13, 2005 02:10 |
| comments on FDM, FEM, FVM, SM, SEM, DSEM, BEM | kenn | Main CFD Forum | 2 | July 18, 2004 18:28 |
| Wall functions | Abhijit Tilak | Main CFD Forum | 6 | February 5, 1999 01:16 |