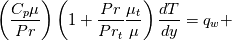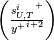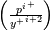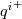|
|||
|
Posted in Uncategorized
Views 731
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 780
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 611
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 678
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 713
Comments 0

|


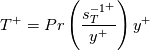
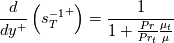
![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T - \frac{d}{dy}\left[\left(\mu+\mu_t\right)U\frac{dU}{dy}\right] \frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T - \frac{d}{dy}\left[\left(\mu+\mu_t\right)U\frac{dU}{dy}\right]](/Forums/vbLatex/img/a4cb00b946f9e49c483e638f60b5b8b5-1.gif)