 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Senior Member
Bernhard
Join Date: Sep 2009
Location: Delft
Posts: 790
Rep Power: 21  |
Hi all,
I have some questions about this same issue with respect to the dynamic Smagorinsky model. I think I am making a mistake somewhere, but please correct me if I am wrong. I've tried to look at other locations for the same issue, but couldn't find it. I compare the dynamic model in OpenFOAM (not caring about the domain averages coefficient) with the dynamic model (described in Lilly and Pope). I think we agree on the following (D defined in OpenFOAM, S common definition) 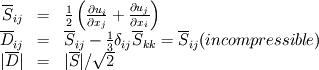 Now, looking at the code (dynSmagorinsky 1.7, homogeneousDynSmagorinsky 2.0), in the .C file at line 57, 62 respectively: ![M_{ij} = \Delta^2 \left[ \widehat{|\overline{D}|\overline{D}_{ij}} - 4 |\widehat{\overline{D}}_{ij}\widehat{\overline{D}}_{ij}|\right] M_{ij} = \Delta^2 \left[ \widehat{|\overline{D}|\overline{D}_{ij}} - 4 |\widehat{\overline{D}}_{ij}\widehat{\overline{D}}_{ij}|\right]](/Forums/vbLatex/img/4ad964a28346a52f96fedb8351df4829-1.gif) as compared to the original of Lilly (in Pope this expression 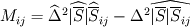 If D_ij=S_ij, but |S|=sqrt(2) |D|, then the second term in the OF implementation is off by a factor sqrt(2). (Where the factor 4 is from the double width of the test filter, and the minus sine is also present in L) Somewhere I must have skipped a step, I hope one of you can point it out for me. Thanks in advance! |
|
|
|

|
|
|
|
|
#22 |
|
Senior Member
Bernhard
Join Date: Sep 2009
Location: Delft
Posts: 790
Rep Power: 21  |
Anybody that can give a comment on this?
|
|
|
|

|
|
|
|
|
#23 |
|
Senior Member
Bernhard
Join Date: Sep 2009
Location: Delft
Posts: 790
Rep Power: 21  |
||
|
|

|
|
|
|
|
#24 | |
|
Member
Gregor Olenik
Join Date: Jun 2009
Location: http://greole.github.io/
Posts: 89
Rep Power: 16  |
Quote:
let symm(gradU) be S, then dev(S) = S - 1/3 trace(S)I however in a incompressible case 1/3 trace(S)I = 0, since trace(S) is the continuity eq. . Therefore in an incrompessible case it doesnt matter whether you take dev(S) or not , but consider a compressible case then 1/3 trace(S) doesn't vanish. In a compressible or variable density case the solver calls divDevRhoBeff to compute the source term due to SGS stress B = 2/3k I - 2 nu_t S_D. (See Fureby http://pof.aip.org/resource/1/phfle6/v9/i5/p1416_s1 Eq. 3) There you have the deviatoric part of D. But i guess openFoam uses nu_t = c Delta^2 ||S_D|| and B = 2/3k I - 2 nu_t S. So it takes S_D for the turbulent viscosity and S for the SGS stress tensor B. |
||
|
|

|
||
|
|
|
#25 | |
|
Senior Member
Join Date: Nov 2012
Posts: 171
Rep Power: 13  |
Quote:
For the compressible Smagorinsky model, the parameters for ck=0.02, ce=1.048 Following the following line: Cs=sqrt(ck*sqrt(ck/ce)) => Cs=0.0525... Does anybody know the references for these specification of the ck and ce for compressible Smagorinsky model? |
||
|
|

|
||
|
|
|
#26 |
|
Member
sqing
Join Date: Sep 2012
Location: Dalian
Posts: 77
Rep Power: 13  |
Hi Yingkun,
As you mentioned, in the incompressible solvers Cs=sqrt(Ck*sqrt(Ck/Ce)). So if I want to set Cs=1, Do I just need to modify Ck and Ce in the LESProperties?Or are there other rules I must obey? Code:
SmagorinskyCoeffs
{
ce 1.05;
ck 0.0472;
}
|
|
|
|

|
|
|
|
|
#27 |
|
Member
Florian Ries
Join Date: Feb 2014
Location: Darmstadt, Germany
Posts: 88
Rep Power: 12  |
Hi Bernhard and everybody,
I compare the dynamic model in OpenFOAM (homoDynSmag OF 2.2.2) with the dynamic model (described in Lilly and Pope) and I have the same Problem. To reanimate the discussion: In Pope (F(.) means filtered): [1] nu_SGS = cS * delta^2 * sqrt(2 * S_ij S_ij) [2] cs = (M_ij L_ij)/(M_kl M_kl) where [3] S_ij = 0.5 (ui,j + uj,i) [4] M_ij = 2 * delta^2 * (F(sqrt(2 * S_ij S_ij) S_ij) - F(sqrt(2 * S_ij S_ij)) F(S_ij)) [5] L_ij = F(ui uj) - F(ui) F(uj) In OF 2.2.2 (homogeneousDySmagorinsky, <.> means averaged): [6] nu_SGS = cD * delta^2 * sqrt(S_ij S_ij) [7] cD = 0.5 (<L_ij M_ij>)/(<M_kl M_kl>) [8] S_ij = D_ij = S_ij Pope [9] M_ij = delta^2 * (F(sqrt(S_kl S_kl) Sij) - 4 * sqrt(<S_kl> <S_kl>) <S_ij>) [10] L_ij = F(ui uj) - F(ui) F(uj) I marked the differences of these models. - First difference is the factor 0.5 in Eq[7] in comparison to Eq[2]. This comes from the factor 2 in Eq[4]. If we put this in Eq[2] we get 0.5 (ok) - Second difference is the different filtering in M_ij. What effect does this have???? (x) - Third difference is the factor 4 in Eq[9] in comparison to Eq[4]. Bernhard: here the factor 4 is from the double width of the test filter can you please explain that?? Why we don`t get a fector in the other filtered terms??? (x) - Fourth difference is the factor 2 in mag(S_ij). (x) In my opinion these models are different or I`m not able to bring the OF-model in the form of pope-model. If it is possible, anyone can please give some advice? kind regards Florian |
|
|
|

|
|
|
|
|
#28 |
|
Senior Member
Freedom
Join Date: May 2014
Posts: 209
Rep Power: 12  |
Quote:
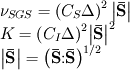 the third one shoub be sqrt(2*Sij*Sij) 
|
|
|
|

|
|
|
|
|
#29 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 15  |
Greetings All
I have performed a Smagorinsky-based compressible LES simulation with the Coefficients as follows: HTML Code:
{
ce = 1.048;
ck= 0.02;
}
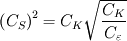 I will get 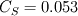 . . My case is a reacting non-premixed combustion with a bluff-body separating fuel and oxidizer streams. I want to change the 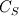 value into 0.13. which value between value into 0.13. which value between 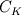 and and 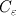 should be modified to retain the nature of the problem? should be modified to retain the nature of the problem?Best, Bobi Last edited by babakflame; December 11, 2014 at 06:45. |
|
|
|

|
|
|
|
|
#30 | |
|
Senior Member
Join Date: Jan 2013
Posts: 372
Rep Power: 14  |
Actually in this paper, we cannot find the information about how the model constants c_k=0.094 and c_{\epsilon}=1.048 come out. So which one is correct reference when I use these two constants? Thanks.
Quote:
|
||
|
|

|
||
|
|
|
#31 |
|
New Member
Liuyue
Join Date: Sep 2015
Posts: 1
Rep Power: 0  |
Hi Lakeat,now I want to write the Scalar SikSkj,but how to write that in openFoam, Thanks.
|
|
|
|

|
|
|
|
|
#32 |
|
New Member
Elyas_Kermani
Join Date: Dec 2015
Location: Iran
Posts: 12
Rep Power: 10  |
hi friends
How can I change the smagorinsky Coeff (Cs) in OF?I want to use Cs=0.1... Regard 
|
|
|
|

|
|
|
|
|
#33 |
|
Member
Jingxue Wang
Join Date: Sep 2017
Posts: 58
Rep Power: 8  |
I read that all the previous posts and reply.
May I understand that Cs=sqrt(Ck*sqrt(2Ck/Ce)) is correct in OpenFoam? Thanks a lot |
|
|
|

|
|
|
|
|
#34 |
|
New Member
Manaf Muhammed
Join Date: Oct 2018
Posts: 20
Rep Power: 7  |
dear madam
As you know the smagorinsky constant Cs in OpenFOAM is defined as a function of Ce and Ck. But when i do the simulation for various combinations of Ck and Ce, that gives the same Cs, I am getting different results. So could you please tell Me where else Ck and Ce is used other than in smagorinsky model. My problem is incompressible LES with standard smagorinsky model and vandriest delta. please help my mailId is manafaero@gmail.com |
|
|
|

|
|
|
|
|
#35 | |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,975
Blog Entries: 45
Rep Power: 128       |
Quote:
__________________
|
||
|
|

|
||
|
|
|
#36 |
|
New Member
Manaf Muhammed
Join Date: Oct 2018
Posts: 20
Rep Power: 7  |
I would like to share some experience of mine regarding the discussion. I also verified the equations given in the discussion. But when i run the simulation for various ck and ce combinations I am getting different results. the nu sgs is not the same in all cases. so eventhough the formula is correct the openFoam is not calculating as per the discussion. Note that I had removed the dependence of k in calculating shear stress B. but still the results differ. So be careful before using this. Also I am a beginner to OpenFOAM and C++. If any body is interested and any comments please post. my mail ID is manafaero@gmail.com.
|
|
|
|

|
|
|
|
|
#37 |
|
Member
George Pichurov
Join Date: Jul 2010
Posts: 52
Rep Power: 15  |
did you check this page with OF implementation https://caefn.com/openfoam/smagorinsky-sgs-model
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Multiphase flow. Dispersed and free surface model | Luis | CFX | 8 | May 29, 2007 18:13 |
| Kato-Launder model | sam | Main CFD Forum | 13 | September 21, 2006 10:15 |
| Kinetic air props model - conductivity HALF? | Chris Bailey | FLUENT | 1 | March 7, 2006 10:38 |
| Reply to Tim Re Dynamic Smagorinsky model | Ajay S. Parihar | Main CFD Forum | 9 | June 2, 2002 16:24 |
| Biharmonic Viscosity with Smagorinsky model | Wen Long | Main CFD Forum | 4 | May 15, 2002 05:54 |