 |
|
|
[Sponsors] | |||||
|
|
|
|
|
#1 |
|
Senior Member
Mahdi Hosseinali
Join Date: Apr 2009
Location: NB, Canada
Posts: 273
Rep Power: 18  |
has anyone calculated taylor microscale in openfoam?
Appreciate it if you share the code. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Mahdi Hosseinali
Join Date: Apr 2009
Location: NB, Canada
Posts: 273
Rep Power: 18  |
any one has any Idea?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Daniel P. Combest
Join Date: Mar 2009
Location: St. Louis, USA
Posts: 621
Rep Power: 0   |
People might be more likely to help if you provide a little more information e.g. equations; sources; what you have tried already; what type of simulation your are performing. I'm interested in the topic if you can provide more details.
Last edited by chegdan; November 21, 2012 at 07:54. Reason: edit: this sounds better |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Mahdi Hosseinali
Join Date: Apr 2009
Location: NB, Canada
Posts: 273
Rep Power: 18  |
thanks for the interest chegdan,
Taylor microscale is the main length scale measured in turbulent homogeneous box to determine Reynolds number since there is no physical length scale. here is a more descriptive of what it naturally is: http://en.wikipedia.org/wiki/Taylor_microscale but a formula to calculate it is presented in "turbulent flow" by Pope in page 199. Can you tell me how to put that formula in Opefoam? |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Daniel P. Combest
Join Date: Mar 2009
Location: St. Louis, USA
Posts: 621
Rep Power: 0   |
Looking at Pope, around the page that you suggested, I find that the longitudinal Taylor microscale
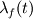 can be related to the transverse Taylor microscale can be related to the transverse Taylor microscale 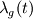 via viawhere However, this formulation seems simplistic compared to the definition by pope using the longitudinal ( 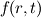 ) and transverse ( ) and transverse (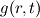 ) autocorrelation functions. If you are looking for those, then I will have to think about this some more. ) autocorrelation functions. If you are looking for those, then I will have to think about this some more.If you are satisfied with the second equation formulation, then I would suggest you look into the post-processing utilities as to how variables are read in at each time and used to calculate what you want e.g. Co utility. Give it a try and post back if you run into problems. |
|
|
|

|
|
 |
|
|