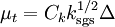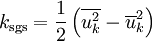Kinetic energy subgrid-scale model
From CFD-Wiki
(Difference between revisions)
m |
m (Reverted edits by CrochIvare (Talk) to last version by Salva) |
| (One intermediate revision not shown) | |
Latest revision as of 09:46, 17 December 2008
The subgrid-scale kinetic energy is defined as
The subgrid-scale stress can then be written as
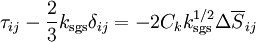
this gives us the transport equation for subgrid-scale kinetic energy
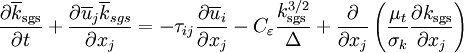
The subgrid-scale eddy viscosity,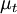 , is computed using
, is computed using 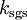 as
as