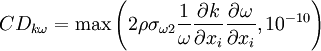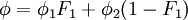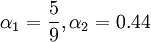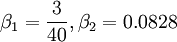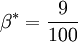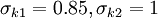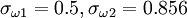SST k-omega model
From CFD-Wiki
The SST k-ω turbulence model [Menter 1993] is a two-equation eddy-viscosity model which has become very popular. The shear stress transport (SST) formulation combines the best of two worlds. The use of a k-ω formulation in the inner parts of the boundary layer makes the model directly usable all the way down to the wall through the viscous sub-layer, hence the SST k-ω model can be used as a Low-Re turbulence model without any extra damping functions. The SST formulation also switches to a k-ε behaviour in the free-stream and thereby avoids the common k-ω problem that the model is too sensitive to the inlet free-stream turbulence properties. Authors who use the SST k-ω model often merit it for its good behaviour in adverse pressure gradients and separating flow. The SST k-ω model does produce a bit too large turbulence levels in regions with large normal strain, like stagnation regions and regions with strong acceleration. This tendency is much less pronounced than with a normal k-ε model though.
Contents |
Kinematic Eddy Viscosity
Turbulence Kinetic Energy
Specific Dissipation Rate
Closure Coefficients and Auxilary Relations
References
- Menter, F. R. (1993), "Zonal Two Equation k-ω Turbulence Models for Aerodynamic Flows", AIAA Paper 93-2906.
- Menter, F. R. (1994), "Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications", AIAA Journal, vol. 32, no 8. pp. 1598-1605.

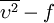 model
model
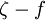 model
model
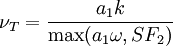
![{{\partial k} \over {\partial t}} + U_j {{\partial k} \over {\partial x_j }} = P_k - \beta ^* k\omega + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma_k \nu _T } \right){{\partial k} \over {\partial x_j }}} \right]](/W/images/math/2/b/1/2b15a566cc406b49688be7eaa8c3215f.png)
![{{\partial \omega } \over {\partial t}} + U_j {{\partial \omega } \over {\partial x_j }} = \alpha S^2 - \beta \omega ^2 + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma_{\omega} \nu _T } \right){{\partial \omega } \over {\partial x_j }}} \right] + 2( 1 - F_1 ) \sigma_{\omega 2} {1 \over \omega} {{\partial k } \over {\partial x_i}} {{\partial \omega } \over {\partial x_i}}](/W/images/math/a/1/3/a134e239a765d4638a74df753866847a.png)
![F_2=\mbox{tanh} \left[ \left[ \mbox{max} \left( { 2 \sqrt{k} \over \beta^* \omega y } , { 500 \nu \over y^2 \omega } \right) \right]^2 \right]](/W/images/math/8/7/d/87d29560b46100813cef49e9f861f1cc.png)
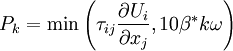
![F_1=\mbox{tanh} \left\{ \left\{ \mbox{min} \left[ \mbox{max} \left( {\sqrt{k} \over \beta ^* \omega y}, {500 \nu \over y^2 \omega} \right) , {4 \sigma_{\omega 2} k \over CD_{k\omega} y^2} \right] \right\} ^4 \right\}](/W/images/math/1/4/3/1438132576e08de1da7394c694172485.png)