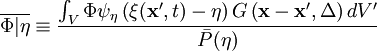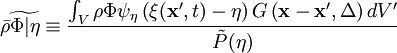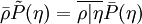Conditional filtering
From CFD-Wiki
A conditional filtering operation of a variable 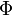 is defined as
is defined as
where 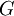 is a positive defined space filter with filter width
is a positive defined space filter with filter width 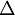 (see LES filters),
(see LES filters),
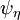 is a fine-grained probability density function,
which is taken as a Dirac delta
is a fine-grained probability density function,
which is taken as a Dirac delta 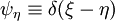 .
The probability density function
.
The probability density function
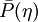 is a subgrid PDF and
is a subgrid PDF and 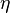 is the sample space of the passive scalar
is the sample space of the passive scalar
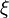 .
In variable density flows, the conditional density-weighted (Favre) filtering is used.
Using the density-weighted PDF ,
.
In variable density flows, the conditional density-weighted (Favre) filtering is used.
Using the density-weighted PDF , 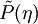 , the conditionally Favre filtered operation is
, the conditionally Favre filtered operation is
The relation between Favre and conventional PDF's is