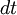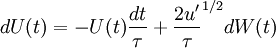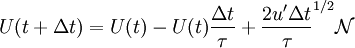Langevin equation
From CFD-Wiki
The stochastic differential equation (SDE) for velocity component 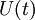 ,
the Langevin equation is
,
the Langevin equation is
where 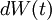 is a Wiener process.
is a Wiener process.
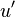 is the turbulence intensity and
is the turbulence intensity and 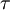 a Lagrangian time-scale.
a Lagrangian time-scale.
Th finite difference approximation of the above equation is
where 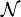 is a standardized Gaussian random variable with 0 mean an unity variance
which is independent of
is a standardized Gaussian random variable with 0 mean an unity variance
which is independent of 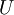 on all other time steps (Pope 1994).
The Wiener process can be understood as Gaussian random variable with 0 mean
and variance
on all other time steps (Pope 1994).
The Wiener process can be understood as Gaussian random variable with 0 mean
and variance