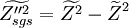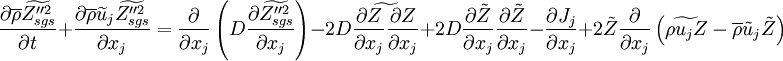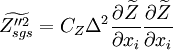Subgrid variance
From CFD-Wiki
The subgrid variance of a passive scalar is defined as
The scalar subgrid variance is also known as the subgrid scalar energy in analogy to the kinetic subgrid energy. An equation for the subgrid variance is
where 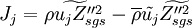 is a subgrid variance flux and is often modeled using a gradient approach with turbulent diffusivity.
is a subgrid variance flux and is often modeled using a gradient approach with turbulent diffusivity.
Instead of solving the above equation, algebraic models are often used. For dimensional analysis
where 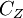 can be obtained from the scalar spectra and its value is 0.1-0.2.
can be obtained from the scalar spectra and its value is 0.1-0.2.