 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Dec 2009
Posts: 8
Rep Power: 16  |
Hi all,
a basic question: What is the mathematical correct definition of omega (specific dissipation rate in the k-omega)? I cannot find a correct answer, anywhere. Also in Wilcox's book it is not mathematically described. Even in all books and publications I got, it is only derived by the turbulent viscosity definition. Is it according to the Baldwin-Lomax as div x c ? Hope, someone has a clue... Thnx, kippo |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Hamid Zoka
Join Date: Nov 2009
Posts: 282
Rep Power: 18  |
Dear Kippo;
omega has a different meaning in k-omega turbulence models. it can be stated as: Epsilon=C*Omega*K in which epsilon is eddy dissipation, K is turbulence kinetic energy and C is the model constant. although in some versions of k-omega C is defined as a function of mean flow strain and rotation rates and omega itself implicitly. regards |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Dec 2009
Posts: 8
Rep Power: 16  |
Thnx a lot,
but this is again all the time the same definition I get. What I mean is the following: To derive the equation for k, you can take the trace of the Reynold-shear-stress tensor. epsilon will occure in the equation in this way: eij=2/rho*avg(du'i*du'j)/(dxjdxj) the k-equation is the trace of the Rij-tensor: Meaning in the k-equation, which can be derrived by avg(u'i*Ns(ui))=0 you will get a dissipation-term like the following (factor 2 is not there, because trace): rho*epsilon=avg(µdu'i*du'i)/(dxjdxj) meaning, epsilon is a tensor built out of the second derivation of the turbulent energy k (correct?). the units for k~m˛/s˛, epsilon~m˛/sł If you look then to the specific dissipation rate omega, as also defined as omega=epsilon/(Cµ*k)~1/T (according to the turbulent viscosity definition), then omega should be mathematically seen a tensor built by the tensors k/epsilon. But what is then the correct mathematic definition. If you look further to the k-omega-SST equations. Menter transformed the epsilon in the k-epsilon to suit the omega-equation. So an additional term occurs in the transformed epsilon-equation: +2*rho/(sigma*omega)*dk/dxj*domega/dxj (this is the cross-diffusion modification, see manuals CFX of Fluent, or StarCD). Where can I derive this term from the epsilon and omega-definition? Or again, what is the correct mathematical definition of omega? thnx a lot, kippo |
|
|
|

|
|
|
|
|
#4 | |
|
Member
annn
Join Date: Jun 2016
Posts: 40
Rep Power: 9  |
Quote:
if so where does the solver get the epsilon value from, since its not calculated in the turbulence model? |
||
|
|

|
||
|
|
|
#5 |
|
New Member
Riccardo
Join Date: Jan 2016
Posts: 16
Rep Power: 10  |
Citing cfd-online:
"There is no strict mathematical definition of the specific turbulence dissipation, 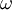 (at least none known by the author, please add one here if you know it). Instead it is most often defined implicitly using the turbulence kinetic energy, (at least none known by the author, please add one here if you know it). Instead it is most often defined implicitly using the turbulence kinetic energy, 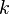 , and the turbulence dissipation, , and the turbulence dissipation,  : : 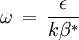 Where 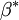 is a model constant, most often set to: is a model constant, most often set to: 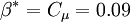 Please note that some models/codes instead use a different definition without the model constant: 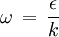 " " So my question is: which is the definition used by FLUENT for defining omega? I wasn't able to find a precise answer to such a question. According to FLUENT user's guide: "which can also be thought of as the ratio of  to to  " makes me think there is not C_mu inside the FLUENT definition...but it is not so clear after all. " makes me think there is not C_mu inside the FLUENT definition...but it is not so clear after all. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Mike
Join Date: Jan 2017
Posts: 2
Rep Power: 0  |
Hi, from the paper by Ferrari et al. CFD study of Savonius wint turbine: 3D model validation and parametric analysis. (Elsevier, Renewable Energy)
Omega= [C_mu^(3/4)]*[ (k^(1/2)) / L] Where C_mu= 0.09 L=0.07*HydraulicDiameter k= (3/2)*[(FlowSpeed*Turbulence Intensity)^2] This is the one I am using for my simulations. Hope this helps. |
|
|
|

|
|
|
|
|
#7 |
|
Member
Join Date: Nov 2018
Posts: 39
Rep Power: 7  |
Can someone explain which specific dissipation rate formulation is more appropriate for OpenFOAM?
1. This: https://www.openfoam.com/documentati...omega-sst.html ω=(Cμ^0.75)*(k^0.5)/L (1) Or this: https://www.simscale.com/docs/simula...s/k-omega-sst/ ω=(k^0.5)/(Cμ^0.25*L) (2) In papers I can see both of them used to guess the initial conditions. One example is the paper by Ferrari et al. mentioned above, using OF. https://www.sciencedirect.com/scienc...via%3Dihub#fd6 I have been using this relation (1) successfully for a while now. Also, do these initial guesses affect the final solution significantly? e.g. will the final wall shear stress be affected? |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,674
Rep Power: 66    |
Quote:
These are the same formula. The difference is that omega is defined differently for (1) versus (2). One uses a definition for omega that contains the model constant Cμ, the other does not. If you are using OpenFOAM, use the OpenFOAM version (1) |
||
|
|

|
||
|
|
|
#9 | |
|
Member
Join Date: Nov 2018
Posts: 39
Rep Power: 7  |
Quote:
Thanks. I switched the links above. The OF formula is the 2nd one, in fact. So I have been using the wrong one... Well, I will run some test to see if it affects the results. The solver has managed to converge with this one: ω=(Cμ^0.75)*(k^0.5)/L In the paper they used it too... |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| turbulent dissipation rate | pluto | STAR-CCM+ | 3 | November 11, 2009 14:41 |
| surface reaction rate | zhou | FLUENT | 4 | October 2, 2003 16:16 |
| TKE SPECTRUM & DISSIPATION | Christian Paukert | Main CFD Forum | 2 | March 14, 2001 19:34 |
| how to decide boundary condition of turbulence energy dissipation rate? | Vincent B. | Main CFD Forum | 5 | October 28, 1999 04:07 |
| calculation of (turbulent) dissipation energy ? | max | Main CFD Forum | 3 | August 18, 1999 09:42 |