 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
sunil
Join Date: Jan 2010
Posts: 8
Rep Power: 16  |
hi,
how to write u . del v or u dot del v in openfoam language for solver modification . here u and v are both vector. please help me. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Pedro Lopes
Join Date: Jun 2012
Location: Coimbra, Portugal
Posts: 4
Rep Power: 13  |
Hi Sunil,
Have you found the answer for your question? Best regards, Pedro |
|
|
|

|
|
|
|
|
#3 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,975
Blog Entries: 45
Rep Power: 128       |
Greetings to all!
I'm not familiar with the operator "del". What exactly is it? Can you provide the expression in LaTeX form (explained here: http://www.cfd-online.com/Forums/sit...ne-forums.html ) or an image of the equation? Best regards, Bruno |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Pedro Lopes
Join Date: Jun 2012
Location: Coimbra, Portugal
Posts: 4
Rep Power: 13  |
Hi Bruno,
I supose that the word "del" means the "nabla"  . . At least this is what makes more sense i.e. 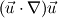 . .Do you know how to solve this term in OpenFOAM? Kind regards, Obrigado, Pedro Last edited by pedromiglopes; November 10, 2014 at 18:19. |
|
|
|

|
|
|
|
|
#5 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,975
Blog Entries: 45
Rep Power: 128       |
Hi Pedro,
 So it is! I found this today by chance on Wikipedia and everything: http://en.wikipedia.org/wiki/Del - weird name they gave it... the first thing that comes to mind is always that it would be a deletion operator, which doesn't make much sense So it is! I found this today by chance on Wikipedia and everything: http://en.wikipedia.org/wiki/Del - weird name they gave it... the first thing that comes to mind is always that it would be a deletion operator, which doesn't make much sense  I don't have enough time right now (this week for that matter  ), so the best I can do is suggest that you study the OpenFOAM Programmer's Guide, which is mentioned here: http://openfoamwiki.net/index.php/Ma...rGuideAddendum ), so the best I can do is suggest that you study the OpenFOAM Programmer's Guide, which is mentioned here: http://openfoamwiki.net/index.php/Ma...rGuideAddendumIt has a lot of information on this topic and that wiki page has already a few fixes for said document. In addition, this comes to mind: http://openfoamwiki.net/index.php/ScalarTransportFoam Good luck! Best regards, Bruno |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Pedro Lopes
Join Date: Jun 2012
Location: Coimbra, Portugal
Posts: 4
Rep Power: 13  |
Hi Bruno, thank you for the tips provided!
After some investigation I think I found the answer. Please correct me if I'm wrong. 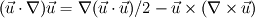 Font: http://pt.wikipedia.org/wiki/Nabla#Identidades (Just the Portuguese version of Wikipedia has this explanation) which in OpenFOAM can be solved as: 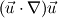 = fvc::grad(U&U)/2 - (U^(fvc::curl(U))) = fvc::grad(U&U)/2 - (U^(fvc::curl(U)))The compilation works at least. Let's wait for the results. Regards, Pedro |
|
|
|

|
|
|
|
|
#7 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,975
Blog Entries: 45
Rep Power: 128       |
Hi Pedro,
Looks good to me! Although the "2" should probably be "2.0", to avoid any accidental intermediate conversions of the calculations in between to integer values. In other words: Code:
fvc::grad(U&U)/2.0 - (U^(fvc::curl(U))) Best regards, Bruno |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello,
Is there any answer to the original question? I think it is related to the convective term in UEqn. In interFoam, we have the annotation: Code:
fvm::div(rhoPhi, U) 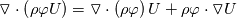 The 1st product RHS term can be further split off: 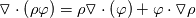 So, we get 2 so called directional derivatives. (Note: 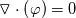 , so one term can be removed) How can we implement this into OpenFoam? I see a potential advantage that U is present both as linear value and derivation, which potentially is faster in integration than just as a gradient. Regards, Daniel |
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
anonymous
Join Date: Aug 2014
Posts: 205
Rep Power: 12  |
Quote:
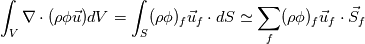 As you can see there is no need to split the divergence term with the chain rule. Although your approximation might be true in the differential form of the momentum equation, one must bare in mind that we are working with the weak form of the equation. Your approximation might also work, but numerically it might introduce instabilities because of the large gradients of the density in the interphase. |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Well,
I know how it is implemented right now. Nevertheless, there may be some benefit in describing the term differently. The original question was how to describe directional derivatives as I understand. If you apply this on the momentum equation, as an example, this may be useful or not. I want to try it out. The reason is that the U field is calculated as if it is a linear function in the momentum equation. The rho phi field contains the quadatic term and must be iterated separatly. This works only if both pEqn and the phi interpolation converge. So, I see the advantage of a potentially faster and more stable iteration. The other point is that the above decribed formulation means that the momnetum equation is split of into a term due to the concentration gradient, the divergence of the flux and the gradient in U. If you remove the divergence of the flux term, you might get a more independent momentum equation (less influenced by the volumetric balance). So, is there a way to describe directional derivatives in OpenFoam or not? I did not find anything of that kind in the user guide. Regards, Daniel |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
It seems that there is no such thing in OpenFoam as
Code:
fvm::grad Code:
&fvm::grad Code:
&fvc::grad There is another area where this could be useful that is viscosity as function of shear rate. Regards, Daniel |
|
|
|

|
|
|
|
|
#12 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,975
Blog Entries: 45
Rep Power: 128       |
Greetings to all!
@Daniel: I've taken a somewhat quick look at your questions and I'm having trouble understanding what is the exact problem!? I ask this because I'm not seeing what is the exact problem of writing the chain expression as explicit equation terms in OpenFOAM's C++ terminology? Best regards, Bruno
__________________
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Hello Bruno,
The explicit expressions are largely covered by OpenFOAM, even though I do not think that directional derivatives are. Or do you know that they are? The implicit schemes are largely limited to fvm::div what I have seen so far. This is a pity since I could imagine that convergence is better if some other fvm schemes would be available. The original question starts ( I have to guess) with the dyad product. My understanding is that the the momentum eq. contains such a dyad product U U. If you apply the divergence of a dyad product, and apply the product rule you get a directional derivative. Maybe look at this: http://planetmath.org/nablaactingonproducts So, I think this is not available within OpenFoam. But you may confirm. Or you think it is anyway a bad idea. Regards, Daniel |
|
|
|

|
|
|
|
|
#14 |
|
Retired Super Moderator
Bruno Santos
Join Date: Mar 2009
Location: Lisbon, Portugal
Posts: 10,975
Blog Entries: 45
Rep Power: 128       |
Hi Daniel,
Well, for better or for worse, this is getting way over my head... possibly because it's the weekend and my brain isn't at full throttle  From what I know, "dyad" operators are not available in OpenFOAM. Beyond that, my guess is that this approach you're referring to will increase the complexity of the equation to be solved, with little benefit in the results. Unfortunately I don't have time to test any of this  . .You can try contacting the OpenFOAM Foundation directly, or proposing this idea at the bug tracker as a possible feature, since they are the experts on this. Beyond this, I vaguely remember seeing that other approaches into multiphase solvers have been talked about in OpenFOAM workshops... you can also check how the multiphase Euler approaches are implemented in OpenFOAM, since those usually require a lot more complex equations... at least from what I briefly remember... Best regards, Bruno |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Daniel Witte
Join Date: Nov 2011
Posts: 148
Rep Power: 14  |
Thanks Bruno,
You are right that there is likely little benefit in this. My original intent was to correct my equations since div(phi) seems never to go down below a certain barrier, around 10^-8. So, I though substracting a div(phi) term or more implicit formulation may help to get the error down. Now, I have found there is another issue. This is really a tricky one, but I think this is the fundamental problem. I would appreciate your help. See http://www.cfd-online.com/Forums/ope...auf-p_rgh.html Have a nice weekend. Regards, Daniel |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Superlinear speedup in OpenFOAM 13 | msrinath80 | OpenFOAM Running, Solving & CFD | 18 | March 3, 2015 05:36 |
| Modified OpenFOAM Forum Structure and New Mailing-List | pete | Site News & Announcements | 0 | June 29, 2009 05:56 |
| 64bitrhel5 OF installation instructions | mirko | OpenFOAM Installation | 2 | August 12, 2008 18:07 |
| Adventure of fisrst openfoam installation on Ubuntu 710 | jussi | OpenFOAM Installation | 0 | April 24, 2008 14:25 |
| OpenFOAM Debian packaging current status problems and TODOs | oseen | OpenFOAM Installation | 9 | August 26, 2007 13:50 |