 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
Hi all,
1.: I´m sure that someone has already figured out how to calculate the electric field strength in openfoam and how to display it with paraview. I´d really appreciate if you could help me with that. 2.: I´m very new to Linux and OpenFoam and currently I´m running the virtual machine version of CAELinux2008 on Windows. So everything should be preinstalled and working, but when I type "wmake" in the console it always says "command not found". So at the moment I´m not getting further with figuring out on my own how to calculate the electric field strength because I can´t compile my own applications. Any idea on the second problem would be appreciated even more. Best regards André |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
Update: Second problem solved. Now to the first one...
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
which solver you are using now? i have i solver to solve the EHD problem.you can get electric field strenth in result, and the solver could be find in OpenFOAM wiki
Regards wayne |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Mariam Winkler
Join Date: Mar 2009
Posts: 4
Rep Power: 17  |
The potential of an electrostatic field is calculated using the poisson equation. I think there are examples in the userguide for this type of equation.
To my knowledge electrodynamics cannot be calculated with openfoam. What is your question about paraview display? Once you calculated the potential, write out it's gradient. Display the magnitude of this gradient, which is the field strength. Regards, Mariam |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
Ok, finally I figured it out now: I added the calculation of the gradient in the .H- and .C-File of electrostaticFoam analogous to the rhoFlux calculation and compiled it. Now I have the electric field as a vector and the magnitude of it in paraview, which is what I wanted.
Salomé, OpenFOAM and paraview are nice tools if you have finally figured out how to work with them ;) Best regards André |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
"To my knowledge electrodynamics cannot be calculated with openfoam."
But it should be possible, shouldn´t it? Or is there already something in work perhaps? |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Michael Jaworski
Join Date: Mar 2009
Location: Champaign, IL, USA
Posts: 126
Rep Power: 17  |
In order to solve electrodynamics problems, you have to solve the full Maxwell wave equations.
The programming guide does include the ability to put in second order time derivatives on page P-37. This and a laplacian are all you need (provided you have the correct boundary conditions and E-B coupling) to solve the wave equation. Alternatively, you only need the laplacian operator if you want to solve time-harmonic fields. c.f. Balanis, "Advanced Engineering Electromagnetics" John Wiley & Sons, 1989. or other suitable text on the topic. Regards, Mike J. |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
Hm, something went wrong. I wanted to add this picture:
 |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
Hi all,
I have done a little step-by-step guide about how to model a simple geometry and solve for its electric field in CAELinux. It´s written for absolute beginners like me. Would be nice if a real beginner could test it sometime and report back if everything worked out. Best regards André |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Andre Kunze
Join Date: Mar 2009
Location: Dresden, Germany
Posts: 7
Rep Power: 17  |
||
|
|

|
|
|
|
|
#11 | ||
|
Senior Member
Michael Jaworski
Join Date: Mar 2009
Location: Champaign, IL, USA
Posts: 126
Rep Power: 17  |
Andre and others,
I have been looking at this capacitance calculation as well and I can't find a source for the discrepancy. I have constructed a much simpler mesh exploiting spherical symmetry and the solver I wrote calculates the field energy a little more simply using only: Quote:
I had also had a hunch that the problem might be numerical accuracy since the resultant energy is on the order of 10<sup>-08</sup>. Rather than solve the phi equation the way it currently is in electrostaticFoam, I have: Quote:
The case that has been constructed is done with blockMesh (all files included below) and models a small wedge taken out of the sphere with arc-lengths of 5 degrees on a side. The bottom and top surfaces are constant phi surfaces (100 and 0) and the sides have a zeroGradient BC. I have used various levels of mesh refinement without much improvement from the results below. The energy/epsilon0 calculated for the case is 0.78461. Multiplying by 1650.1 scales the energy value from the wedge to full sphere and the calculated capacitance is 2.2926 pF. The analytical result is 2.2253pF, a difference of 3%. I have tried to go through various fvSolution tolerance levels (currently at 1e-10) and fvSchemes but the solution never gets below a 3% error. So, is 3% error as good as this can get? Any thoughts on this matter would be greatly appreciated. Regards, Mike J. |
|||
|
|

|
|||
|
|
|
#12 | ||
|
Senior Member
Michael Jaworski
Join Date: Mar 2009
Location: Champaign, IL, USA
Posts: 126
Rep Power: 17  |
Andre and others,
I have been looking at this capacitance calculation as well and I can't find a source for the discrepancy. I have constructed a much simpler mesh exploiting spherical symmetry and the solver I wrote calculates the field energy a little more simply using only: Quote:
I had also had a hunch that the problem might be numerical accuracy since the resultant energy is on the order of 10<sup>-08</sup>. Rather than solve the phi equation the way it currently is in electrostaticFoam, I have: Quote:
The case that has been constructed is done with blockMesh (all files included below) and models a small wedge taken out of the sphere with arc-lengths of 5 degrees on a side. The bottom and top surfaces are constant phi surfaces (100 and 0) and the sides have a zeroGradient BC. I have used various levels of mesh refinement without much improvement from the results below. The energy/epsilon0 calculated for the case is 0.78461. Multiplying by 1650.1 scales the energy value from the wedge to full sphere and the calculated capacitance is 2.2926 pF. The analytical result is 2.2253pF, a difference of 3%. I have tried to go through various fvSolution tolerance levels (currently at 1e-10) and fvSchemes but the solution never gets below a 3% error. So, is 3% error as good as this can get? Any thoughts on this matter would be greatly appreciated. Regards, Mike J. Solver files case files Mesh Image |
|||
|
|

|
|||
|
|
|
#13 | |
|
New Member
Xingzhi You
Join Date: May 2010
Posts: 7
Rep Power: 15  |
Hi Mike,
I get one question on the electrostatic foam, and hope you can give some thoughts and help. First, what is k in rhoFlux = -k*mesh.magSf()*fvc::snGrad(phi) . I checked the dimension of it and: k [-1 0 2 0 0 1 0 ] 0.00016 which means the unit is kg-1· s2 ·A, this is not the electric conductivity unit as simens per meter would be m-3·kg-1·s3 ·A2. And we can restructure it to be (kg-1S2A)(ASm-3), and ASm-3 is just Cm-3(coulomb per cubic meter). It seems k is electric conductivity divided charge density, which makes it unknown to me. Furthermore,where does that weird 0.00016 come from, it is not any familiar constant or electric property. Second, in rhoFlux = -k*mesh.magSf()*fvc::snGrad(phi) equation, the mesh.magSf() gives the magnitude of surface cell area. So rhoFlux would be, if not talk about the k, then surface area times potential gradient(at the surface normal, which is electric field), which gives: (electric_conductivity/charge_density)*(area)*(electric_field) = current/charge-density This is so weird. Then what does solve fvm::ddt(rho) + fvm::div(rhoFlux, rho) means? Best regards, Hans Quote:
|
||
|
|

|
||
|
|
|
#14 |
|
New Member
Vincent de Graaf
Join Date: Jun 2010
Location: Germany
Posts: 12
Rep Power: 15  |
k is the ion mobility or electric mobility, which is defined by Vd=k*E. Vd is the drift velocity in m/s, k is the electric mobility and E the electric field strength. The drift velocity is the physical speed at which the charge carriers travel through the medium.
The unit of k is m^2/(Vs) which is equal to As^2/kg. |
|
|
|

|
|
|
|
|
#15 | |
|
New Member
Xingzhi You
Join Date: May 2010
Posts: 7
Rep Power: 15  |
Quote:
|
||
|
|

|
||
|
|
|
#16 |
|
Senior Member
Daniele
Join Date: Feb 2010
Posts: 134
Rep Power: 16  |
Hi
I'm trying to use electrostaticFoam. I would use it to simulate an elctroforming cell to calculate Nickel deposit thikness. So I must calculate charge density on my cathode and from that I can obtain deposit thikness. But in electrostaticFoam I must impose rho on my cathode. Is this the correct way to solve my problem: 1) I Solve Laplace equation (I impose potential on my surface) 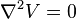 2) I compute electric field 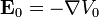 3) I obtain charge density on my surface with Coulomb theorem: 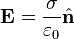 It's correct? Thanks |
|
|
|

|
|
|
|
|
#17 |
|
Senior Member
Mieszko Młody
Join Date: Mar 2009
Location: POLAND, USA
Posts: 145
Rep Power: 17  |
Dear Foamers,
I am trying to solve for electric potential inside the capacitor. But how can I calculate the charge density at the boundary ? Is the charge density zero, or non-zero value in between the capacitor plates ? thanks ZMM |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| UDF-electric field | Srinivas | Fluent UDF and Scheme Programming | 20 | August 29, 2017 15:16 |
| electric field | Alexandra Mutzke | CFX | 6 | November 1, 2012 13:50 |
| Electric Field calculation | JamesT | Phoenics | 5 | May 31, 2007 04:44 |
| electric field in star-cd | yong | Siemens | 0 | November 16, 2004 07:43 |
| How to calculate grad Electric Potential? | Miko | CFX | 5 | October 14, 2003 09:02 |