 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Vincent
Join Date: Jul 2011
Posts: 29
Rep Power: 14  |
This post is in response to a message I recieved of someone that wanted to have a more detailed explanation on how to obtain the non-dimensional NS equations. Since others might be interested (and the fact that I like this tex compiler) I posted on this forum.
For starters we introduce the Navier Stokes equations and look at the x-direction component: 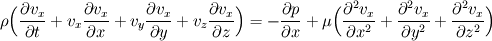 We assume no additional body forces. The components of the velocity field v are denoted by subscripts (x,y,z). The pressure is given by p and  is the density. is the density.First we divide by the density  in order to simplify the equation. in order to simplify the equation.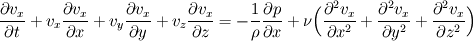 The reader should check that indeed each terms has a dimension equal to 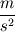 . Now in order to obtaint the non-dimensional equation we make the following substitutions. . Now in order to obtaint the non-dimensional equation we make the following substitutions.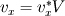 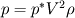 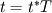 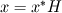 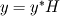 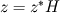 Quantities with a superscript star are dimensionless quantities and the capital letters V and H have dimensions  and and 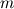 respectively. respectively. Please check that these substitutions are indeed valid. For instance the physical length is 4 m. We decide to take the length H equal to 1 m, giving a non-dimensionalised length of 4. Using the above substitutions we end up with the following equation: 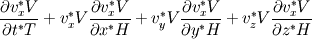 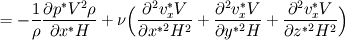 We simplify this equation and use that T = H/V. 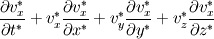 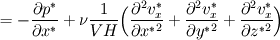 Here 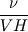 is our inverse reynolds number. is our inverse reynolds number.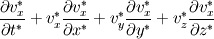 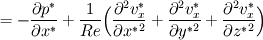 Where Re is defined as 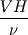 . Now we have non-dimensionalised the NS equations. Please rememeber that if you solve this equation you will end up with the nondimensionalised quantities. In order to revert them to physical quantities you will need to use the equation we proposed above when we non-dimensionalised the quantities. . Now we have non-dimensionalised the NS equations. Please rememeber that if you solve this equation you will end up with the nondimensionalised quantities. In order to revert them to physical quantities you will need to use the equation we proposed above when we non-dimensionalised the quantities.Good luck! Regards, Vincent |
|
|
|

|
|
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Filtered navier stokes equation..LES:: | Palani Velladurai | Main CFD Forum | 7 | September 6, 2013 02:51 |
| Adding a term to Navier Stokes Equation | ashtonJ | CFX | 3 | January 15, 2011 06:32 |
| Navier stokes compresible viscid flow fea, somebody can help? | Jose Choy | Main CFD Forum | 3 | October 24, 2003 02:28 |
| Newbie:Viscoelasticity and Navier stokes equation | Rajil Saraswat | Main CFD Forum | 2 | June 9, 2003 07:21 |
| help: I am trying to solve Navier Stokes compressible and viscid flow | Jose Choy | Main CFD Forum | 2 | May 18, 2000 05:45 |