 |
|
|
[Sponsors] | |||||
Correction procedure on a non-orthogonal skewed Mesh |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Mohamed Elshahat Ouda
Join Date: May 2010
Posts: 29
Rep Power: 16  |
Dear All,
I need your help to understand the procedure to apply the required corrections for both non-orthogonality and skewness in OpenFOAM both from theoretical and implementation point of view. I'll illustrate my understanding from theoretical point of view to discuss it. If it is correct we can proceed to the implementation aspects. Image below illustrate a skewed non-orthogonal mesh  The discretized diffusion term in cell P can be written as: 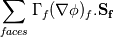 On a non orthogonal mesh, the following partitioning for face normal vector is usually done: 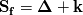 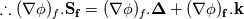 ........ (1) ........ (1)Where the first term of the previous equation is the orthogonal contribution which evaluated implicitly, and the second term is the non-orthogonality correction term which evaluated explicitly in a deferred manner. To calculate those terms we start by interpolating the the face variable: 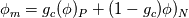 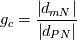 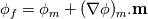 ........ (2) ........ (2)Where the last term in the previous equation is the skewness correction. Taking the gradient of the last equation we get: 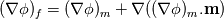 Then substituting in equation (1) we get: 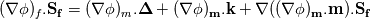 ........ (3) ........ (3)Equation (3) should be the final form. Different terms in this equation are calculated as follows: First term is calculated implicitly: 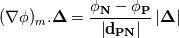 Second term is the non-orthogonality correction term. This term is evaluated explicitly in a deferred manner. This means that the face gradient is evaluated explicitly based on the current cell centred gradient as: 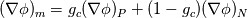 The cell centred gradient itself is calculated explicitly using e.g. Gauss theory as: 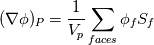 In the previous equation the variable value at face is calculated using equation (2) (obviously many loops are needed). I've no clue how to evaluate the third term in equation (3) So first, is this solution correct theoretically? Is it the same as implemented in OpenFOAM? and what about the third term? Best regards. Last edited by me.ouda; January 18, 2017 at 16:59. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| sliding mesh problem in CFX | Saima | CFX | 46 | September 11, 2021 07:38 |
| [snappyHexMesh] Snappyhex mesh: poor inlet mesh | Swagga5aur | OpenFOAM Meshing & Mesh Conversion | 1 | December 3, 2016 16:59 |
| [mesh manipulation] Importing Multiple Meshes | thomasnwalshiii | OpenFOAM Meshing & Mesh Conversion | 18 | December 19, 2015 18:57 |
| [GAMBIT] how to generate orthogonal mesh using GAMBIT? | ivanbuz | ANSYS Meshing & Geometry | 8 | October 21, 2009 03:41 |
| Convergence moving mesh | lr103476 | OpenFOAM Running, Solving & CFD | 30 | November 19, 2007 14:09 |