 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Reine Granström
Join Date: Apr 2009
Location: Sweden
Posts: 43
Rep Power: 17  |
Dear all,
I am trying to compare the wall function implementation in CFX and Fluent, and there are a few things I don't understand from reading the documentation. The problem is as follows: As I understand it, at least in CFX the reason for using the form of nondimensionalized distance and velocity having superscript "*" rather than "+" is due to the law of the wall becoming singular at separation points. The definition of the dimensionless wall distance y* is the same in both codes: 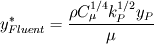 , , 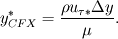 Also, the dissipation Also, the dissipation  is calculated by the same expression in both codes. is calculated by the same expression in both codes.First, in CFX the friction velocity 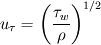 is replaced by is replaced by 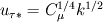 (eq. 2.222) to get rid of the singularity issue. My interpretation is that the following is then done: (eq. 2.222) to get rid of the singularity issue. My interpretation is that the following is then done:In Fluent on the other hand, a dimensionless velocity 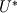 is defined by: is defined by: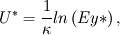 (eq. 4.12-1) (eq. 4.12-1)where 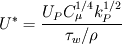 (eq. 4.12-2) (eq. 4.12-2)My guess is that the latter expression is used for the same reason as (eq. 2.222) is used in CFX, i.e. to cope with the singularity issue. My interpretation is that the following is done in Fluent: I assume that 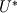 is equivalent to is equivalent to 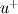 in the law of the wall, in the same way as (eq. 2.222) is equivalent to the friction velocity in the law of the wall, in the same way as (eq. 2.222) is equivalent to the friction velocity 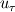 . .If the dimensionless velocity in CFX (equivalent to Fluent's 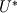 ) is ) is 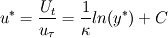 . Then, it seems to me that the wall function implementation differs between the codes. Are they different, or have I misunderstood something? . Then, it seems to me that the wall function implementation differs between the codes. Are they different, or have I misunderstood something?I appreciate any comments. Last edited by gravis; May 5, 2010 at 03:07. Reason: Rephrasing and corrections |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| modelling wall thickness coupling (like fluent) in cfx | suryawanshi_nitin | CFX | 3 | April 13, 2009 01:25 |
| Fluent and CFX | Ale | CFX | 1 | July 2, 2008 18:19 |
| Fluent and CFX | Ale | FLUENT | 0 | July 1, 2008 08:36 |
| Fluent Vs CFX, density and pressure | Omer | CFX | 9 | June 28, 2007 04:13 |
| CFX function in Fluent | Andrew | FLUENT | 4 | December 11, 2006 08:44 |