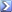Wave Action Equation Solver for OpenFOAM
Posted September 3, 2013 at 07:18 by egp
Hi Tom,
This sounds like an interesting problem! Ignoring the wave space issue for a moment, I think you need to first cast the problem as a 2D surface using either the finiteArea machinery of 1.6-ext, or the thin film model in 2.2.x (see reactingParcelFilmFoam).
The wave space issue is a bit more complex and I don't have a good recommendation for an elegant solution. Brute force for a fixed number of wave-space bins would be doable, but ugly. What is the typical wave-space discretization in other codes such as WaveWatch III http://polar.ncep.noaa.gov/waves/wavewatch/
Good luck,
Eric
This sounds like an interesting problem! Ignoring the wave space issue for a moment, I think you need to first cast the problem as a 2D surface using either the finiteArea machinery of 1.6-ext, or the thin film model in 2.2.x (see reactingParcelFilmFoam).
The wave space issue is a bit more complex and I don't have a good recommendation for an elegant solution. Brute force for a fixed number of wave-space bins would be doable, but ugly. What is the typical wave-space discretization in other codes such as WaveWatch III http://polar.ncep.noaa.gov/waves/wavewatch/
Good luck,
Eric
Quote:
Originally Posted by chyczewski
I need to develop a solver for the wave action equation using the OpenFOAM library and am very interested in any insights veteran users might have on the best way to get this done.
The wave action equation is of the following form:
where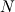
is the wave action which is a function of geographical space 
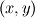, wavenumber magnitude 
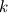and wavenumber direction 
.
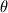(The wave action is related to the ocean wave height spectra and this equation governs the evolution of this spectra in the presence of nonuniform currents and winds).
My first question is, does anyone know of any implementations of a solver for an equation like this in OpenFOAM?
My suspicion is that the answer to my first question is 'no' (though I hope I'm wrong). So, I've been thinking of how I will do this and this is what I've come up with:
This equation can be solved using a fractional step method:
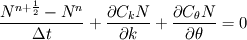
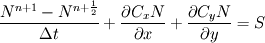
The first step is local in geographic space, including only derivatives in wavespace, which is discretized in a simple structured manner. So the first step can be completed sequentially for each point in geographical space.
Then the second step can be solved sequentially in wavenumber space using the features of the OpenFOAM library to solve the equation that contains only geographical space terms. This would require, for each point in wavenumber space, copying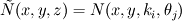
, where 
is a third dimension added to fit the OpenFOAM framework. So, actually, 
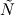is solved in the second set for all 
.
Assuming this approach makes sense, can someone outline how I would create a volume scalar field array with two added dimensions to represent the wavenumber space so that I can simply specify a point in wavenumber space (i.e.) to be copied to a volume scalar field that can be processed in OpenFOAM? Once that is accomplished I think the only other thing to contend with is how to apply the boundary conditions to the second step equation, which are a function of the position in wavenumber space. Though it doesn't seem to daunting, I haven't completely thought it through yet.
Any insights or suggestions would be greatly appreciated.
Tom
The wave action equation is of the following form:
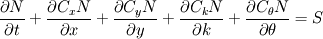
where
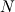is the wave action which is a function of geographical space 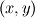, wavenumber magnitude 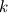and wavenumber direction 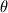.(The wave action is related to the ocean wave height spectra and this equation governs the evolution of this spectra in the presence of nonuniform currents and winds).
My first question is, does anyone know of any implementations of a solver for an equation like this in OpenFOAM?
My suspicion is that the answer to my first question is 'no' (though I hope I'm wrong). So, I've been thinking of how I will do this and this is what I've come up with:
This equation can be solved using a fractional step method:
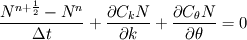
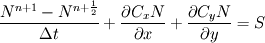
The first step is local in geographic space, including only derivatives in wavespace, which is discretized in a simple structured manner. So the first step can be completed sequentially for each point in geographical space.
Then the second step can be solved sequentially in wavenumber space using the features of the OpenFOAM library to solve the equation that contains only geographical space terms. This would require, for each point in wavenumber space, copying
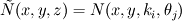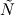, where is a third dimension added to fit the OpenFOAM framework. So, actually, is solved in the second set for all .Assuming this approach makes sense, can someone outline how I would create a volume scalar field array with two added dimensions to represent the wavenumber space so that I can simply specify a point in wavenumber space (i.e.
) to be copied to a volume scalar field that can be processed in OpenFOAM? Once that is accomplished I think the only other thing to contend with is how to apply the boundary conditions to the second step equation, which are a function of the position in wavenumber space. Though it doesn't seem to daunting, I haven't completely thought it through yet.Any insights or suggestions would be greatly appreciated.
Tom
Total Comments 0
