Unofficial theory guide for relativeVelocityModel in OpenFOAM8 (OpenFOAM.org)
Posted September 19, 2022 at 12:58 by nepomnyi
Updated September 23, 2022 at 12:56 by nepomnyi (I continue where I stopped yesterday.)
Updated September 23, 2022 at 12:56 by nepomnyi (I continue where I stopped yesterday.)
Tags openfoam
Here's the theory for relativeVelocityModel in OpenFOAM8 that I uncovered manually going through the code and commit history of OpenFOAM8.
Before we proceed, since there are a couple of main scientific schools in the world that use different notation, let me declare some notations that I'm going to be using:
<-- this dot is just a general sign for multiplication; both multiplication of scalars and scalar multiplication of vectors can be denoted by it; obviously, if I multiply vectors, I will denote them as vectors (i.e. with an arrow above), everything that doesn't have an arrow above is a scalar
and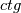 
are tangent and cotangent respectively
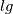is logarithm with the base of 10
is natural logarithm
, 
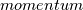and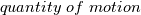 
are all the same thing
General idea
If we want to describe a two-phase gas-liquid or liquid-liquid flow mathematically, we write the Navier-Stokes for each phase. That's the general consensus of fluid mechanics community (though, I, personally, do not absolutely agree with it).
Such a system of equations is difficult to solve. Therefore, people started simplifying the equations - even throwing away some equations - by, of course, simplifying the physics of the flow they want to describe.
Such systems of equations are called reduced order models. Note, that when you simplify and throw away the equations, you end up having less equations than unknowns in general. Therefore, people try to come up with so called closure relations that are meant to be very simple (preferably, linear algebraic equations) and bring the total number of equations to the total number of unknowns.
That changes the flow physics a lot, but gives you general understanding of the flow behavior. In other words, that doesn't give you the details of the flow but, rather, gives you general characteristics of the flow.
One of such models is called drift-flux model. Its closure relation is called slip relation.
Drift-flux model is one of those models that simplifies the physics to the highest degree possible. It's not suitable for detailed flow description. But if, for instance, you are interested in an approximate pressure drop in a several kilometers deep oil well, that's your model of choice. It will give general understanding of what pumps to use and the cost of running it is very low.
The theory of the drift-flux model was developed by Mamoru Ishii, an emeritus professor at Purdue.
The development of the slip relation started before Mamoru Ishii, but he made a significant contribution to it. The slip relation is used on its own sometimes.
Mamoru Ishii, Takashi Hibiki, "Thermo-fluid dynamics of two-phase flow", 2nd edition, 2011, Springer is the fundamental book on the modeling of two-phase flows in general and the drift-flux model in particular.
The reduction of the physics in the drift-flux model is briefly described by the following. What if one imagines a fluid-fluid flow as the flow of fully diluted gas mixture for which the theory is well developed. One can do that, but should do something with the fact that as opposed to a gas mixture, a bubble in water moves relative to the water due to buoyancy. The theory of gas mixture flow doesn't account for that. Therefore, one must amend the theory of gas mixture flow to account for the drift (slip) velocity of bubbles if he wants to apply that theory to bubbly flows (or other two-phase flows).
In order to account for that, one should use the slip relation.
One of the main parameter in the slip relation is drift velocity. There are many empirical equations for the drift velocity.
OpenFOAM offers the choice of two equations for the drift velocity.
Those equations are accessible under the relativeVelocityModels in OpenFOAM.
NOTE: I have a suspicion that OpenFOAM means something else under driftFluxFoam, I'm still investigating that.
relativeVelocityModels
The structure of the code behind relativeVelocityModels is shown here.
You can choose between simple and general drift velocity models.
Note, that in C++, you use two-file system. In .H files, you declare variables and functions. In .C files, you assign values and expressions to the variable and functions declared in .H files.
Therefore, the formula for the simple drift velocity model is shown in the file simple.C, see line 66. It was declared in the file simple.H, see line 90.
The simple drift velocity model goes as follows:
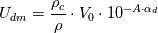
The formula for the general drift velocity model is shown in the file general.C, see line 67. It was declared in the file general.H, see line 93.
The general drift velocity model goes as follows:
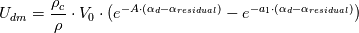
The names of some of the parameters in these formulas are:
Instead, these equations are pretty much the same in OpenFOAM10 (the differences are negligible). And OpenFOAM10 commit history readily gives you the commit where the reference to the article is given.
Thus, these equations and their parameters are after Michaels, Bolger, "Settling rates and sediment volumes of flocculated kaolin suspensions", 1962, Industrial and engineering chemistry fundamentals, 1(1), p.24-33. See this commit in the OpenFOAM10 general.C file.
Once I've found the article, it became clear to me that the drift velocity models used in driftFluxFoam are designed for liquid-liquid flows, where one of the liquids should better be non-Newtonian mud (sludge, slurry).
It became clear to me why all the driftFluxFoam tutorials are focused on liquid-liquid scenarios. Especially, dahl tutorial that talks about sludge and water.
That is sufficient knowledge for me at this point, because I'm working with gas-liquid flows, closure relations for which are different from liquid-liquid flows. That is why I didn't look deeper into the theory of the presented closure relations for drift velocity and, thus, I'm not talking about them here. Dear community members with the knowledge on them, please, provide them in the comments and I'll amend the blog.
I'm turning my attention to the main system of equations that constitutes driftFluxFoam.
I've been digging them out from the code for several days already to no success so far. Once I'm ready, I'll post them in another blog entry.
Before we proceed, since there are a couple of main scientific schools in the world that use different notation, let me declare some notations that I'm going to be using:
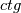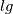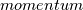<-- this dot is just a general sign for multiplication; both multiplication of scalars and scalar multiplication of vectors can be denoted by it; obviously, if I multiply vectors, I will denote them as vectors (i.e. with an arrow above), everything that doesn't have an arrow above is a scalar and are tangent and cotangent respectively is logarithm with the base of 10 is natural logarithm, and 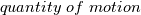are all the same thingGeneral idea
If we want to describe a two-phase gas-liquid or liquid-liquid flow mathematically, we write the Navier-Stokes for each phase. That's the general consensus of fluid mechanics community (though, I, personally, do not absolutely agree with it).
Such a system of equations is difficult to solve. Therefore, people started simplifying the equations - even throwing away some equations - by, of course, simplifying the physics of the flow they want to describe.
Such systems of equations are called reduced order models. Note, that when you simplify and throw away the equations, you end up having less equations than unknowns in general. Therefore, people try to come up with so called closure relations that are meant to be very simple (preferably, linear algebraic equations) and bring the total number of equations to the total number of unknowns.
That changes the flow physics a lot, but gives you general understanding of the flow behavior. In other words, that doesn't give you the details of the flow but, rather, gives you general characteristics of the flow.
One of such models is called drift-flux model. Its closure relation is called slip relation.
Drift-flux model is one of those models that simplifies the physics to the highest degree possible. It's not suitable for detailed flow description. But if, for instance, you are interested in an approximate pressure drop in a several kilometers deep oil well, that's your model of choice. It will give general understanding of what pumps to use and the cost of running it is very low.
The theory of the drift-flux model was developed by Mamoru Ishii, an emeritus professor at Purdue.
The development of the slip relation started before Mamoru Ishii, but he made a significant contribution to it. The slip relation is used on its own sometimes.
Mamoru Ishii, Takashi Hibiki, "Thermo-fluid dynamics of two-phase flow", 2nd edition, 2011, Springer is the fundamental book on the modeling of two-phase flows in general and the drift-flux model in particular.
The reduction of the physics in the drift-flux model is briefly described by the following. What if one imagines a fluid-fluid flow as the flow of fully diluted gas mixture for which the theory is well developed. One can do that, but should do something with the fact that as opposed to a gas mixture, a bubble in water moves relative to the water due to buoyancy. The theory of gas mixture flow doesn't account for that. Therefore, one must amend the theory of gas mixture flow to account for the drift (slip) velocity of bubbles if he wants to apply that theory to bubbly flows (or other two-phase flows).
In order to account for that, one should use the slip relation.
One of the main parameter in the slip relation is drift velocity. There are many empirical equations for the drift velocity.
OpenFOAM offers the choice of two equations for the drift velocity.
Those equations are accessible under the relativeVelocityModels in OpenFOAM.
NOTE: I have a suspicion that OpenFOAM means something else under driftFluxFoam, I'm still investigating that.
relativeVelocityModels
The structure of the code behind relativeVelocityModels is shown here.
You can choose between simple and general drift velocity models.
Note, that in C++, you use two-file system. In .H files, you declare variables and functions. In .C files, you assign values and expressions to the variable and functions declared in .H files.
Therefore, the formula for the simple drift velocity model is shown in the file simple.C, see line 66. It was declared in the file simple.H, see line 90.
The simple drift velocity model goes as follows:
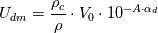
The formula for the general drift velocity model is shown in the file general.C, see line 67. It was declared in the file general.H, see line 93.
The general drift velocity model goes as follows:
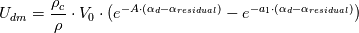
The names of some of the parameters in these formulas are:
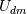is called diffusion velocity, see, e.g., general.H line 92
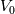is called drift velocity, see, e.g., general.H line 63
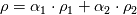is declared in the createFields.H file (see line 57), which is a part of interPhaseChangeFoam, and not the part of driftFluxFoam.
Instead, these equations are pretty much the same in OpenFOAM10 (the differences are negligible). And OpenFOAM10 commit history readily gives you the commit where the reference to the article is given.
Thus, these equations and their parameters are after Michaels, Bolger, "Settling rates and sediment volumes of flocculated kaolin suspensions", 1962, Industrial and engineering chemistry fundamentals, 1(1), p.24-33. See this commit in the OpenFOAM10 general.C file.
Once I've found the article, it became clear to me that the drift velocity models used in driftFluxFoam are designed for liquid-liquid flows, where one of the liquids should better be non-Newtonian mud (sludge, slurry).
It became clear to me why all the driftFluxFoam tutorials are focused on liquid-liquid scenarios. Especially, dahl tutorial that talks about sludge and water.
That is sufficient knowledge for me at this point, because I'm working with gas-liquid flows, closure relations for which are different from liquid-liquid flows. That is why I didn't look deeper into the theory of the presented closure relations for drift velocity and, thus, I'm not talking about them here. Dear community members with the knowledge on them, please, provide them in the comments and I'll amend the blog.
I'm turning my attention to the main system of equations that constitutes driftFluxFoam.
I've been digging them out from the code for several days already to no success so far. Once I'm ready, I'll post them in another blog entry.
Total Comments 0
