Flux computation in unstructured grids
Posted July 16, 2010 at 10:49 by praveen
Tags finite volume, unstructured
Consider finite volume scheme on unstructured grids for the Euler equations.
Let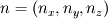
be normal to a cell face and whose magnitude is equal to face area. Let 
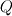be the conserved vector. The finite volume update equation using forward Euler time discretization is
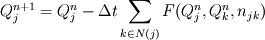
Here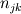
is a normal vector pointing from current cell "j" into the neighbouring cell "k". Note that the conserved variable Q is updated in the global Cartesian coordinate frame.
As an example, the Rusanov flux would be defined as
![F(U,V,n) = \frac{1}{2}[ F(U) \cdot n + F(V) \cdot n] - \frac{1}{2} \lambda(U,V,n) (V - U)](/Forums/vbLatex/img/afbf757e031082087c6c22031139a5e1-1.gif "F(U,V,n) = \frac{1}{2}[ F(U) \cdot n + F(V) \cdot n] - \frac{1}{2} \lambda(U,V,n) (V - U)")
Here, we have used the definition
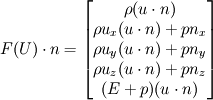
where
is the velocity vector, etc., and
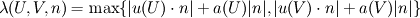
with
being speed of sound. Note that there are many other ways to define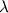 
.
Let
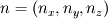be normal to a cell face and whose magnitude is equal to face area. Let 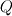be the conserved vector. The finite volume update equation using forward Euler time discretization is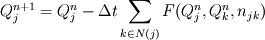Here
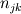is a normal vector pointing from current cell "j" into the neighbouring cell "k". Note that the conserved variable Q is updated in the global Cartesian coordinate frame.As an example, the Rusanov flux would be defined as
Here, we have used the definition
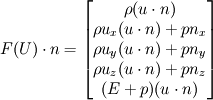
where
is the velocity vector, etc., and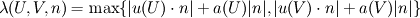with
being speed of sound. Note that there are many other ways to define .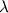
Total Comments 0
