Physical Aspects of Lagrangian Particle Tracking (DPM)
Posted March 1, 2020 at 05:41 by vinerm
Tags dpm, lagrangian, lpt
This blog is first of the two part blog related to DPM Modeling. It is not to be considered as a professional document. Nor is it meant for those who consider themselves to be expert in DPM. It is meant as a guide for the beginners who want to understand various aspects related to DPM Modeling. Though terminology is meant to be general but it is rather closer to the one used in Fluent. Of course, experts are also welcome to go through it and share their comments.
Assume that there is a need to track the evolution of contaminant in a canal. There are at least two ways to do it. Place a few sensors at a few locations. Or attach a sensor to multiple boats and let them traverse the canal. The latter is called Lagrangian.
The boats may or may not have any drives to control their motion. Now these boats may be very small and light, just like the paper boats from the childhood. These will go with the flow without disturbing the flow of the water in any noticeable manner. This is known as One-Way coupling in DPM or LPT terminology. Or, these could be boats with rotors or big in size or heavy in mass and, consequently, the flow of the canal will be affected due to their presence. Even the distribution of the contaminant could be affected. This is called Two-Way coupling.
Now, imagine having these big or heavy boats instead of light ones. Or it could be mix as well. But, if there are too many boats in the canal, a wave generated by one will affect the motion of all the nearby boats. That is three-way coupling. And if their number increases so much that it feels like traffic on the road, boats hitting each other, literally, to the extent that its not the flow rather the hits that decide the motion, you have what is called four-way coupling. This is where models like DEM come into play.
Some users think of DEM as a separate model than DPM. The reality is that particles are always tracked using DPM but when there are so many of these that the forces generated due to their hits with each other affect their motion, some model is required to predict this force. DEM predicts that force.
Lets consider one of these heavy boats. What are the bare minimum forces acting on it.
1. Its mass or weight, if you like the latter term, pulling it towards the center of the earth
2. The resistance from the air as well as water, only water if it is a submarine. This is called drag force and depends on various aspects, such as, contact area with the fluid, surface roughness, shape, and presence of other boats or submarines around it. The method to address three-way coupling is actually addition of extra forces or modification of drag due to this presence of extra particles around the particle being tracked. And there is lift along with the drag; always normal to the drag.
3. A large wave could also push the boat in a particular direction. Essentially, a wave brings a pressure difference because of its height and boat is pushed from higher pressure to lower pressure. This is called the pressure gradient force.
4. Other types of forces could be generated by rolling of the boat, its rotor at the back, or if it being towed. There is buoyancy that is pushing it up.
For particles, that are not as big as boats, even smaller than paper boats, other forces also need to be considered. But before we go into that, lets take a look at the shape of the particles.
As far as LPT is concerned, particles are assumed to have spherical shape. But particles are also termed as point particles. So, how is spherical shape important. Or how is shape important at all. To rephrase it, how is the shape taken into account. Its via the exchange coefficients, the models that define how a particle and the continuous fluid around it exchange various fields, such as, momentum, mass, thermal energy, etc.
If drag model for a sphere is used, then it is obvious that the user is assuming the particles to be sphere. But lets say that the user wants to assume the particles to be oblong spheres or cylinders. Can he use drag coefficient for the cylinder or for oblong sphere? Ideally, yes. Practically, there are a few issues.
Since LPT tracks only the positions of the particles, their orientations are unknown. Drag for a cylinder will certainly depend on its orientation. As far as sphere is concerned, it is invariant under rotations, i.e., it does not matter about which axis you rotate it, as long as the axis is passing through its center, its orientation will not vary. So, a single drag coefficient can be applied to all particles. For oblong spheres, their orientation is required but is unavailable.
One plausible approach would be to use some probability distribution function for the orientation of the particles and apply drag or other forces based on that. But usually, it is not justified because the particles are much smaller than the characteristic length scale of the flow.
Mass and heat transfer are also affected by the orientation. Though the area for drag force, or reaction, or heat convection remains the same, Nusselt and Sherwood numbers do not. They are affected by the orientation just like drag and lift coefficient. Therefore, particles are usually assumed or expected to be spherical or slightly non-spherical for applicability of DPM.
Another important aspect is the volume fraction. Remember the waves from one boat affecting the flow of nearby boats. Well, standard DPM is valid until that happens. In other words, DPM is valid for use if the volume occupied by the particles is so less that they do not affect their neighbors in any significant manner. Usually, it is assumed that if the particles occupy less than 10% volume, then the LPT is valid. Do note that this condition needs to be satisfied locally as well as globally, i.e., if one cell has one particle then the cell volume should be at least 10 times the particle volume. There is no such limit on mass loading or mass fraction though.
Now, these particles have to come from somewhere. That is what is called Injection. The injections require the important parameters to be specified, such as, initial position and velocity vectors, diameter for the calculation of mass and area (remember it is a sphere), total mass flow rate, temperature (if temperature is important for the simulation and thermal energy equation is being solved), and time duration for the injection.
Now, there is no number specified here. CFD tools determine this number by taking a ratio of mass flow rate and mass of each particle, which is based on material property and diameter. Usually, this turns out to be in millions. Since each particle requires one equation, and this will be captured in the part two, millions of equations need to be solved. Now, that's expensive.
Solution is to use representative particles, or otherwise known as parcels. Each parcel can depict any number of particles, varying from 1 to hundreds of thousands. This makes the situation workable. But what are basis for this? There are particles that have similar momentum or similar mass or similar position, or some other similarity that can be exploited to track them together. And that's how parcels are tracked. This number can be controlled by the user.
So, once the tool knows the initial conditions, provided via injections, and it knows the forces acting on it, all that remains is to solve a rather simple ODE, called Newton's second law.
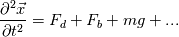
As you observe, the equation has only one independent variable, time. So, the particle tracking is always transient. Solution procedure for this and the setup for DPM in Fluent will make the second part of this blog. Do not expect a tutorial, rather aspects that need to be looked after while setting it up.
Until next time...
Assume that there is a need to track the evolution of contaminant in a canal. There are at least two ways to do it. Place a few sensors at a few locations. Or attach a sensor to multiple boats and let them traverse the canal. The latter is called Lagrangian.
The boats may or may not have any drives to control their motion. Now these boats may be very small and light, just like the paper boats from the childhood. These will go with the flow without disturbing the flow of the water in any noticeable manner. This is known as One-Way coupling in DPM or LPT terminology. Or, these could be boats with rotors or big in size or heavy in mass and, consequently, the flow of the canal will be affected due to their presence. Even the distribution of the contaminant could be affected. This is called Two-Way coupling.
Now, imagine having these big or heavy boats instead of light ones. Or it could be mix as well. But, if there are too many boats in the canal, a wave generated by one will affect the motion of all the nearby boats. That is three-way coupling. And if their number increases so much that it feels like traffic on the road, boats hitting each other, literally, to the extent that its not the flow rather the hits that decide the motion, you have what is called four-way coupling. This is where models like DEM come into play.
Some users think of DEM as a separate model than DPM. The reality is that particles are always tracked using DPM but when there are so many of these that the forces generated due to their hits with each other affect their motion, some model is required to predict this force. DEM predicts that force.
Lets consider one of these heavy boats. What are the bare minimum forces acting on it.
1. Its mass or weight, if you like the latter term, pulling it towards the center of the earth
2. The resistance from the air as well as water, only water if it is a submarine. This is called drag force and depends on various aspects, such as, contact area with the fluid, surface roughness, shape, and presence of other boats or submarines around it. The method to address three-way coupling is actually addition of extra forces or modification of drag due to this presence of extra particles around the particle being tracked. And there is lift along with the drag; always normal to the drag.
3. A large wave could also push the boat in a particular direction. Essentially, a wave brings a pressure difference because of its height and boat is pushed from higher pressure to lower pressure. This is called the pressure gradient force.
4. Other types of forces could be generated by rolling of the boat, its rotor at the back, or if it being towed. There is buoyancy that is pushing it up.
For particles, that are not as big as boats, even smaller than paper boats, other forces also need to be considered. But before we go into that, lets take a look at the shape of the particles.
As far as LPT is concerned, particles are assumed to have spherical shape. But particles are also termed as point particles. So, how is spherical shape important. Or how is shape important at all. To rephrase it, how is the shape taken into account. Its via the exchange coefficients, the models that define how a particle and the continuous fluid around it exchange various fields, such as, momentum, mass, thermal energy, etc.
If drag model for a sphere is used, then it is obvious that the user is assuming the particles to be sphere. But lets say that the user wants to assume the particles to be oblong spheres or cylinders. Can he use drag coefficient for the cylinder or for oblong sphere? Ideally, yes. Practically, there are a few issues.
Since LPT tracks only the positions of the particles, their orientations are unknown. Drag for a cylinder will certainly depend on its orientation. As far as sphere is concerned, it is invariant under rotations, i.e., it does not matter about which axis you rotate it, as long as the axis is passing through its center, its orientation will not vary. So, a single drag coefficient can be applied to all particles. For oblong spheres, their orientation is required but is unavailable.
One plausible approach would be to use some probability distribution function for the orientation of the particles and apply drag or other forces based on that. But usually, it is not justified because the particles are much smaller than the characteristic length scale of the flow.
Mass and heat transfer are also affected by the orientation. Though the area for drag force, or reaction, or heat convection remains the same, Nusselt and Sherwood numbers do not. They are affected by the orientation just like drag and lift coefficient. Therefore, particles are usually assumed or expected to be spherical or slightly non-spherical for applicability of DPM.
Another important aspect is the volume fraction. Remember the waves from one boat affecting the flow of nearby boats. Well, standard DPM is valid until that happens. In other words, DPM is valid for use if the volume occupied by the particles is so less that they do not affect their neighbors in any significant manner. Usually, it is assumed that if the particles occupy less than 10% volume, then the LPT is valid. Do note that this condition needs to be satisfied locally as well as globally, i.e., if one cell has one particle then the cell volume should be at least 10 times the particle volume. There is no such limit on mass loading or mass fraction though.
Now, these particles have to come from somewhere. That is what is called Injection. The injections require the important parameters to be specified, such as, initial position and velocity vectors, diameter for the calculation of mass and area (remember it is a sphere), total mass flow rate, temperature (if temperature is important for the simulation and thermal energy equation is being solved), and time duration for the injection.
Now, there is no number specified here. CFD tools determine this number by taking a ratio of mass flow rate and mass of each particle, which is based on material property and diameter. Usually, this turns out to be in millions. Since each particle requires one equation, and this will be captured in the part two, millions of equations need to be solved. Now, that's expensive.
Solution is to use representative particles, or otherwise known as parcels. Each parcel can depict any number of particles, varying from 1 to hundreds of thousands. This makes the situation workable. But what are basis for this? There are particles that have similar momentum or similar mass or similar position, or some other similarity that can be exploited to track them together. And that's how parcels are tracked. This number can be controlled by the user.
So, once the tool knows the initial conditions, provided via injections, and it knows the forces acting on it, all that remains is to solve a rather simple ODE, called Newton's second law.
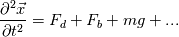
As you observe, the equation has only one independent variable, time. So, the particle tracking is always transient. Solution procedure for this and the setup for DPM in Fluent will make the second part of this blog. Do not expect a tutorial, rather aspects that need to be looked after while setting it up.
Until next time...
Total Comments 1
Comments
-
 Hi vinerm,
Hi vinerm,
thanks a lot for this blog article! It is a good start to better understand DPM!
Is the second part somewhere? I would be interested to read it but couldn't find it.
Regards
mojoPosted April 30, 2021 at 06:10 by Mojo 





