 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Hello,
I am trying to streamline the mesh independence practices using Grid Convergence Index and Richardson Extrapolation as they are considered the best in practical CFD. (Ref: Roache, P. J. "Perspective: a method for uniform reporting of grid refinement studies." TRANSACTIONS-AMERICAN SOCIETY OF MECHANICAL ENGINEERS JOURNAL OF FLUIDS ENGINEERING 116 (1994): 405-405.) Now, element sizes for the consecutive meshes should be known to get the grid refinement ratio used in the calculations in this procedure. But since we use unstructured mesh along with the extruded mesh; I am not sure if the value of element local element size (in the important regions of high gradients) is representative of the size for that particular mesh. Roache suggests the following formula for grid refinement ratio  for unstructured meshes, using their element-counts for unstructured meshes, using their element-counts 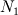 and and 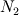 : :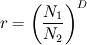 Now, he defines D as Dimensionality. What does it mean and how to calculate it from the fluid domain??  Thanks OJ |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,781
Rep Power: 143     |
You would have to read the paper for the definition of D. But I suspect it will be 2 for 2D models and 3 for 3D models.
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Thanks Glenn.
The only definition Roache gives of D is Dimensionality! But a little more research online after posting my query here landed me to some references that reciprocate the similar definition that you mentioned. Dimensionality is the no. of principle directions in which there is a significant variation of the results. Essentially, a 2D case can have single dimensionality if there are gradients only in single directions. If I may ask, do you personally recommend this method for mesh independence when it comes to unstructured meshes? Or you rely on more general methods of assessing the parameters of interest from results of successive meshes and choose the mesh when you see no significant variation in them? The only problem in this approach is there seems to be no agreed quantification of word "significant". In this paper, Richardson's extrapolation takes into account the results of meshes that are successively refined and then extrapolates this to predict the value of result at zero grid spacing (i.e. continuum). At the same time, the Grid Convergence Index helps understand if the results generated in the current successive meshes are sufficiently close to the asymptotic range, where any refinement in the mesh won't result in significant change in results. This way we not only ensure the mesh independence but also predict the numerical solution at continuum. Obviously, there will be a difference between actual result and numerical result at continuum, but then, CFD is about getting the best results within its caveats. Regards OJ |
|
|
|

|
|
|
|
|
#4 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,781
Rep Power: 143     |
The definition of significant is what you define as significant. If you are doing initial design calcs then 20% error might be fine - you just want a general ida of what is going on. But for final design work you might want 5% error. Or if you are doing detailed turbomachinery work then 1% error is suiable.
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Thanks. When you say 5% change in solution by refinement, what is the refinement ratio for the mesh size?
I go a bit detailed. If 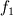 and and 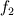 are the solutions of two successive meshes ( are the solutions of two successive meshes ( 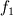 smaller), then is the error you mentioned, say smaller), then is the error you mentioned, say 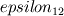 , must be following: , must be following: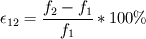 The fundamental problem with this, accordign to Roahce, is that this error doesn't take into account the refinement ratio  and the global order of accuracy and the global order of accuracy 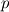 , which is typically smaller than the local order of accuracy of stencil used for discretization, due to grid stretching and quality, non-linearities and assumptions in turbulence modelling etc. , which is typically smaller than the local order of accuracy of stencil used for discretization, due to grid stretching and quality, non-linearities and assumptions in turbulence modelling etc. The Roache then defines Grid Convergence Index which takes into account these uncertainties as: 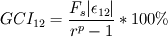 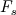 being the factor of safety, 3 for two meshes, 1.25 for three meshes used. In case of three meshes, the GCI for second and third mesh can be given similarly as: being the factor of safety, 3 for two meshes, 1.25 for three meshes used. In case of three meshes, the GCI for second and third mesh can be given similarly as: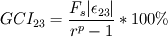 Finally, with the relation 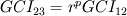 , if the both sides are close to each other, it can be concluded that the meshes are in asymptotic range! The refinement ratio , if the both sides are close to each other, it can be concluded that the meshes are in asymptotic range! The refinement ratio  is easy to calculate from the formula I mentioned in earlier post, and Roache suggests a minimum value of 1.1. So method is not too much demanding either. is easy to calculate from the formula I mentioned in earlier post, and Roache suggests a minimum value of 1.1. So method is not too much demanding either.Thoughts? OJ |
|
|
|

|
|
|
|
|
#6 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,781
Rep Power: 143     |
I did not make myself clear enough in my previous post. I was commenting on your quote "The only problem in this approach is there seems to be no agreed quantification of word "significant".
For some people or cases the detailed analysis of Roache is not possible or practical so they fall back to the simple sensitivity analysis approach of two meshes with significnatly different meshes, and keep refining until the difference between two successive refinements in the parameters of interest (drag, lift, pressure drop, whatever is important) is less than an accuracy tolerance you are happy with. Roache's approach does not require this as it checks you are in the convergent region and if so extrapolates to zero mesh. This is obviously a much better approach. So my 5% was referring to changes in parameters of interest, not of changes in mesh size. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Thanks, I understood that 5% was for the change in parameters of interest. I was asking about what should be percentage change in mesh sizes (% change in no. of elements for unstructured mesh) that you suggest for the two successive meshes in consideration

|
|
|
|

|
|
|
|
|
#8 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,781
Rep Power: 143     |
Oh - Roache gives guidelines on this as well.
But I generally double or halve the length dimension of the element. So a single hex element would become 8 for a 3D model, then 64. Often you are limited in how far you can take this before you run out of capacity, so one model is just "as big as I can fit in". |
|
|
|

|
|
|
|
|
#9 |
|
Member
Thiago Parente Lima
Join Date: Sep 2011
Location: Diamantina, Brazil.
Posts: 62
Rep Power: 14  |
Hi all,
I know this is an old topic, but, once I found it searching for grid convergence strategies, I think other people will drop here as well. Therefore, I want to share this very didatic post about how to estabilish grid convergence: https://curiosityfluids.com/2016/09/...d-convergence/ Hope it helps.
__________________
Fields of interest: buoyantFoam, chtMultRegionFoam. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| how to set periodic boundary conditions | Ganesh | FLUENT | 15 | November 18, 2020 06:09 |
| [snappyHexMesh] Weird snapping outside a refinement region | jasimpson89 | OpenFOAM Meshing & Mesh Conversion | 0 | July 29, 2012 20:46 |
| [snappyHexMesh] Boundary layer in a pipe | Clementhuon | OpenFOAM Meshing & Mesh Conversion | 6 | March 12, 2012 12:41 |
| pressure eq. "converges" after few time steps | maddalena | OpenFOAM Running, Solving & CFD | 69 | July 21, 2011 07:42 |
| How to control Minximum mesh space? | hung | FLUENT | 7 | April 18, 2005 09:38 |