 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Jan 2011
Posts: 1
Rep Power: 0  |
Hi all,
I know that the solver Yplus is used in the wall function during calculation. Recently, I read CFX Theory guide and i found that the solver Yplus of Scalable wall function is based on 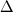 n/4 n/4 and that of Automatic wall treatment is based on 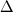 n. n.Where 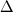 n is physical distance between first and second nodes from wall boundary. n is physical distance between first and second nodes from wall boundary.Since CFX generates its control volumes around each mesh node including boundary nodes, it makes sense that Scalable wall function uses 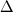 n/4 for wall distance. n/4 for wall distance.However, why does Automatic wall treatment adopt 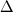 n as wall distance for the solver Yplus? n as wall distance for the solver Yplus? I referred [Chapter 2.8.1.2 Solver Yplus and Yplus, CFX Theory guide, (p. 143)]. No helpful explanation was found in the documentation. I hope to have an answer from wise man... Thank you in advance. Best regards, H. Chung |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Mr CFD
Join Date: Jun 2012
Location: Britain
Posts: 361
Rep Power: 15  |
Wall functions are extremely useful in reducing computational expense as you don't need to model up to the near wall region.
I'm not sure what you mean when you ask: Quote:
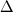 n as a measure makes sense as it's the first cell height between two nodes which is used to calculate Y+. If Y+ is large the solver will use wall functions. If Y+ is small the solver will try to resolve near wall flow. Off course this depends on mesh, type of models used etc. n as a measure makes sense as it's the first cell height between two nodes which is used to calculate Y+. If Y+ is large the solver will use wall functions. If Y+ is small the solver will try to resolve near wall flow. Off course this depends on mesh, type of models used etc.So you're asking why does automatic wall treatment adopt 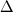 n as the wall distance in the Y+ calculation. Well what measure would you use to determine the wall distance? n as the wall distance in the Y+ calculation. Well what measure would you use to determine the wall distance? 
|
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
You might know that wall functions are valid only when the first grid points are placed at certain distances from wall, below which the velocity profiles are modeled mathematically instead of NS equations. Now, this limit is generally at the y+ values of 11, below which viscous sublayer exists. If you keep refining your grid, your first grid point may as well go well below this distance, falling into viscous layer and hence it gives incorrect shear calculation on the surface, inducing inaccuracy. Hence, scalable wall functions enforce a minumum limit of y+ as
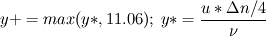 . If you observe, here, u* is used instead of . If you observe, here, u* is used instead of 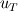 , the shear velocity that is commonly used in all textbooks, because in logarithmic layer the reduction in wall velocity is very rapid. Use of u* which is empirically defined, doesn't let , the shear velocity that is commonly used in all textbooks, because in logarithmic layer the reduction in wall velocity is very rapid. Use of u* which is empirically defined, doesn't let 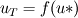 go to close to zero. go to close to zero.Essentially, all these precautions are taken, so that mesh is always beyond viscous sublayer. Here, as you mentioned since CFX puts half control volume around nodes on boundary, the 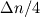 seems a legit value for considering the NS equation involvement, below which wall function takes over. seems a legit value for considering the NS equation involvement, below which wall function takes over.Automatic wall function is a different game. Here, if you use coarse mesh so that the first mesh point is beyond viscous sublayer, wall function is triggered. If you use fine mesh, keeping y+ values smaller than 11 such that the grid points are now within viscous sublayer, the wall function is abandoned and the integration is now untill the wall with the resolution you have with the mesh. Hence the name - Automatic! Now, for first mesh point beyond sublayer the calculations are modelled using y+ (keeping it minimum 11) and for first mesh point within sublayer, which is laminar, the calculations are modelled using simple 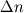 . With automatic wall function, since the first point may lie within or beyond the sublayer, there is no limit imposed on what should be minimum y+ (or the distance first grid point) and hence the mathematical treatment is combination of both definitions and is simply based on . With automatic wall function, since the first point may lie within or beyond the sublayer, there is no limit imposed on what should be minimum y+ (or the distance first grid point) and hence the mathematical treatment is combination of both definitions and is simply based on 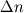 . .OJ |
|
|
|

|
|
 |
| Tags |
| automatic wall treatment, cfx, solver yplus |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [Other] Contribution a new utility: refine wall layer mesh based on yPlus field | lakeat | OpenFOAM Community Contributions | 58 | December 23, 2021 02:36 |
| Automatic wall treatment in CFX | Chander | CFX | 13 | May 6, 2017 00:45 |
| Enhanced wall treatment and Enhanced wall functions | Alina | FLUENT | 2 | January 3, 2012 18:48 |
| Problem Interface Solid Fluid with wall velocity Solver v12 | hills1 | CFX | 2 | October 12, 2009 05:36 |