 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
NormalVector
Join Date: Oct 2010
Posts: 71
Rep Power: 15  |
I'm trying to understand the discretization blending factor Fluent has available (accessible through TUI solve/set/numerics). From what I see in the Fluent users' manual, a value of 0 will use a first order discretization while a value of 1 will "recover higher order discretization." It notes that in order to use it effectively, one of the higher order schemes must be selected for the desirable variables. Does that mean that I have to use at least a second order discretization for density, momentum, etc. in order for the blending to work properly?
I'm having convergence troubles at second order upwind so I'm trying to squeeze all the accuracy I can out of first order. 
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Astio Lamar
Join Date: May 2012
Location: Pipe
Posts: 186
Rep Power: 14  |
Hi!
I have the same question. Do you find any answer? Thanks. |
|
|
|

|
|
|
|
|
#3 |
|
Member
NormalVector
Join Date: Oct 2010
Posts: 71
Rep Power: 15  |
Nope, never did. I just pushed through second order by changing the relaxation factors.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Yes you do need to have a second (or higher order) solution in order to be able to use the blending factor. In very simplistic terms, blending factor B can be defined as:
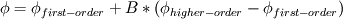 Here  is the quantity like velocity, pressure etc. is the quantity like velocity, pressure etc. Now, if you have a look at the equation, if B=0, we have results of first order and if B=1, we have results of higher order. But if you don't have a higher order solution, then 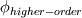 becomes becomes 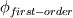 , and for any value of B, you get the solution the same as , and for any value of B, you get the solution the same as 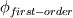 . .Hence it is necessary to have a second or higher order solution in order to use blending factor. It is healthy to go gradually from first order to different blending factors (0.4, 0.7) etc depending on your unstability and then switch to second order, if you are having problems with direct second order solutions. OJ |
|
|
|

|
|
|
|
|
#5 |
|
New Member
JK
Join Date: Jun 2016
Posts: 3
Rep Power: 10  |
Hello everyone,
It is exactly as oj.bulmer stated. When you have a blending factor of 1 active, the code uses all the settings specified under Spatial discretization in the Methods panel. On the other hand, when you use a BF of 0, the code always uses the first order upwind no matter what a scheme you specified. So, setting up a BF between 0 and 1 basically specifies interpolation between these schemes. A BF can, in some circumstances, help with oscillations which you can observe when you are using a higher order scheme. However, one should bare in mind that some accuracy is always lost. Therefore, you can think of the BF as a trade-off between numerical stability and accuracy of the solution. In my experience, by using a BF between 0 and 1, I was able to smooth out some oscillations in the solution variables, however I always got a less accurate solution, and the numerical value of the monitored variable was always between the values I got for the pure 1st Order or Higher order scheme. In some cases, I rather used a transient solver, which sometimes served a very similar purpose.Hope it might be helpful to someone. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| First order simulation better than second order | Torque_Converter | CFX | 7 | January 8, 2013 04:07 |
| How to compute UDS fourth order gradient | Emma66 | FLUENT | 1 | April 27, 2010 05:44 |
| Higher Order FV Schemes for unstructured meshes | Apurva Shukla | Main CFD Forum | 4 | December 15, 2000 09:17 |
| Gradient Estimation for Higher Order Schemes | jianxia | Main CFD Forum | 0 | June 6, 2000 19:40 |
| Higher order FVM | Sergey Smirnov | Main CFD Forum | 10 | April 15, 2000 01:49 |