 |
|
|
[Sponsors] | |||||
Solving a Laplace equation for a scalar quantity |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Ali
Join Date: Mar 2011
Posts: 27
Rep Power: 15  |
Hello,
I am trying to solve 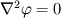 , i.e. homogeneous Laplace equation, in which , i.e. homogeneous Laplace equation, in which 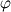 is a scalar quantity and is described in a zone(2D or 3D). We know boundary values of is a scalar quantity and is described in a zone(2D or 3D). We know boundary values of 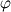 in borders of the zone. This problem is very analogous to head conduction at steady state, yet in borders of the zone. This problem is very analogous to head conduction at steady state, yet 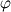 is the electric potential here, not temperature. is the electric potential here, not temperature.I am wondering how to implement this problem in FLUENT. I think I have to mesh the zone and use a udf or something like that. Thanks for your help. |
|
|
|

|
|
|
|
|
#3 |
|
Member
MarkClarence
Join Date: Jul 2014
Posts: 32
Rep Power: 12  |
Hi Amir,
Can you elaborate your statement? How can we justify that unsteady and convective terms can be ignored for solving the laplace equation? (i need to find the change in electric field in my geometry) I think you know how my geometry looks like :P , I have to find the electric field in the rotor domain. If possible can you share the UDF with me? Thank you. -Mark |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
|
Quote:
"UDS" is "User-Defined Scalar" equation and is available in FLUENT, something like energy equation and totally different from "UDF"! In the process of enabling a UDS, you can manage the unsteady and convective terms. For more info, please refer to the manual. Bests,
__________________
Amir |
||
|
|

|
||
|
|
|
#5 |
|
New Member
|
Hi,
Can we solve defined scalar in x, y, z direction separately (for 3D geometry) or how can we see the scalar values in x y z directions using post processing? Regards Tharanga |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
|
Quote:
For sure you cannot solve it separately, but if you want to see the scalar values in a specified direction, you can simply draw a line and plot the scalar values over it... Bests,
__________________
Amir |
||
|
|

|
||
|
|
|
#7 |
|
New Member
|
Hey, Thank you for the reply. I have solved the laplace eq (3D) and I need to get surface integration over x y z direction (separately) . Is there any method for that? cheers
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
|
If I elaborate more, I cant choose from the drop down menu x-scalar values etc. Therefore, I'm struggling to find x y z values over a surface. Thank you.
|
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 26  |
With a user defined scalar, you calculate a scalar, not a vector.
A scalar does not have a x-component... So your question does not make any sense. If you solved an electrostatic problem, your scalar is probably the electric potential. Which component do you want? The x-component of the electric field? You should know the relation between those two. |
|
|
|

|
|
|
|
|
#10 |
|
New Member
|
It is a homogenized flow problem. Ultimately, I need to solve laplace eqn (vector) with BC's . Yes, you are right but there is no other way (I think) than UDS method in fluent to solve Laplace. Please suggest me an alternative method. Thank you
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 26  |
You don't make clear why you need another way. What is wrong with the UDS method?
And are you sure you want a vector laplace equation??? That is very unusual. I don't know why a "homogenized flow problem" would lead to a vector variant of the laplace equation. |
|
|
|

|
|
|
|
|
#12 |
|
New Member
|
Hi, Thank you very much for your kind replies. I solved it as three different problems in fluent. I got the results.
 Regards, Tharanga |
|
|
|

|
|
 |
| Tags |
| electric potential, heat conduction, laplace equation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How to write k and epsilon before the abnormal end | xiuying | OpenFOAM Running, Solving & CFD | 8 | August 27, 2013 15:33 |
| Orifice Plate with a fully developed flow - Problems with convergence | jonmec | OpenFOAM Running, Solving & CFD | 3 | July 28, 2011 05:24 |
| On the damBreak4phaseFine cases | paean | OpenFOAM Running, Solving & CFD | 0 | November 14, 2008 21:14 |
| Convergence moving mesh | lr103476 | OpenFOAM Running, Solving & CFD | 30 | November 19, 2007 14:09 |
| Could anybody help me see this error and give help | liugx212 | OpenFOAM Running, Solving & CFD | 3 | January 4, 2006 18:07 |