[ksq]

Hi all, I'm taking an introductory CFD course, and was hoping for a better explanation than my professor gave for a question I had during class:

When fluid flow is treated as incompressible and isothermal, the energy equation does not need to be solved. I get that this is the case, but what is the reason behind this/why is this the case? (constant temp = constant internal energy? or am I missing a few steps?)

On a related note, what are the major assumptions that we make in this case to reduce the complete set of NS equations to the NS equations for the case for incompressible, isothermal flow? (constant density, anything else?)

[FMDenaro]

Originally Posted by ksq

Hi all, I'm taking an introductory CFD course, and was hoping for a better explanation than my professor gave for a question I had during class:

When fluid flow is treated as incompressible and isothermal, the energy equation does not need to be solved. I get that this is the case, but what is the reason behind this/why is this the case? (constant temp = constant internal energy? or am I missing a few steps?)

On a related note, what are the major assumptions that we make in this case to reduce the complete set of NS equations to the NS equations for the case for incompressible, isothermal flow? (constant density, anything else?)

For incompressible flows, homogeneous density and isothermal condition, the NS equations reduce to

Div V =0
DV/Dt + Grad p = ni* Lap V

that is a set of two equations in two unknowns. The problem is well posed by simply specifying initial and bc.s conditions, you can see that pressure is not a thermodinamic function. The temperature field (i.e., the energy equation) is totally decoupled from the dynamic of the flow.

That can be found in any book of fluid mechanics

[ksq]

The 4 CFD books I looked into just said that it was the case to not solve the energy equation under isothermal conditions, not WHY it was the case. Thanks for your help!

[Jochen]

if you consider the NS equations in the differential form for isothermal and incompressible conditions the derivatives of all temperature and densities equal zero. doing that you can easily derive it yourself.

[FMDenaro]

Originally Posted by Jochen

if you consider the NS equations in the differential form for isothermal and incompressible conditions the derivatives of all temperature and densities equal zero. doing that you can easily derive it yourself.

Maybe, some difference in definitions can confuse me... I assume the suffix "iso" as the same as used for iso-entropic flows. That means that a quantity is constant along trajectory. Thus, for isothermal flows, I assume something like dT/dt+u*dT/dx=0, not necessarily to have all the derivatives zero. I would say the latter case as omo-thermal...

[michujo]

Originally Posted by ksq

The 4 CFD books I looked into just said that it was the case to not solve the energy equation under isothermal conditions, not WHY it was the case. Thanks for your help!

Hi, here's my attempt at explaining it:

1) In a compressible flow, the local density of the fluid depends both on pressure and temperature. The mass, momentum and energy conservation equations are coupled (density appears in all of them!) and therefore they must be solved simultaneously. Pressure is usually calculated from temperature and density using an appropriate equation of state (ideal gas for instance).

2) If you assume incompressible flow (think of a liquid, or even a gas but flowing at a low Mach number) density is constant. The velocity field does not depend anymore on the temperature distribution (since temperature variations do not induce density changes, and also neglecting fluid viscosity dependence on temperature). Therefore, the momentum equation can be solved separately, where pressure is such that it ensures continuity (mass conservation, ).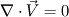
The energy (temperature) equation can be solved for a posteriori using the solved velocity field to obtain the temperature distribution, even though if your fluid is also assumed to be isothermal then there's no need (T=Tfluid everywhere).

Cheers,
Michujo.

[Jochen]

Originally Posted by FMDenaro

Maybe, some difference in definitions can confuse me... I assume the suffix "iso" as the same as used for iso-entropic flows. That means that a quantity is constant along trajectory. Thus, for isothermal flows, I assume something like dT/dt+u*dT/dx=0, not necessarily to have all the derivatives zero. I would say the latter case as omo-thermal...

It is my understanding that isothermal means T=constant everywhere. never heard of omothermal though