 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Dinanath Sharma
Join Date: Aug 2013
Location: India
Posts: 10
Rep Power: 12  |
Hello,
I'm running a two-way coupled simulation of bubbly flow. For the two-way coupling, I'm using Climent and Magnaudet's relation (attaching an image of it). I have already run a 2-d simulation of this case and am now running a 3-d simulation of it. If you can see the equation, there is an added source term to solve for the continuous phase, which has a (Vi/Vf) term multiplied inside the summation. Here Vf is the the control volume of the element and Vi is the total volume of all bubbles present inside the control volume. Now, when I run the 2-d case, I assume the Vf to be (dx*dy*(1)) (1 being unit length in the z direction). For the 3-d case, Vf becomes (dx*dy*dz). Now since Vf for 3-d is a lot lower, compared to the 2-d case, the source term (proportional to Vi/Vf) is much higher for the 3-d case. Since the velocity of the bubbles depends on the velocity of the surrounding continuous phase, my 3-d bubbles are moving much faster compared to the 2-d case. The 2-d result matches much more with experimental results than the 3-d case. Can anyone tell me where I'm possibly going wrong? How to rectify this problem. If anyone has an experience with handling two phase flows, please help me out. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Dinanath Sharma
Join Date: Aug 2013
Location: India
Posts: 10
Rep Power: 12  |
Reminder
I don't want a concrete reply. Even if you have any rough ideas about this, please post it. Thanks |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
||
|
|

|
|
|
|
|
#4 |
|
New Member
Dinanath Sharma
Join Date: Aug 2013
Location: India
Posts: 10
Rep Power: 12  |
For the 2-d case, I am using
Vi/Vf = (πD3/6)/(Δx·Δy·L) where L is the length of the tank in z direction (from the experiment of the same setup) For 3-d, I am using Vi/Vf = (πD3/6)/(Δx·Δy·Δz) Do you mean to say that I should use Vi/Vf = (πD2/4)/(Δx·Δy) for 2-d and Vi/Vf = (πD3/6)/(Δx·Δy·Δz) for 3d? Even in that case, won't the two terms not necessarily be the same? |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi,
Sorry but I don't think I understand your problem. Can you please state it more clearly? What I am saying is that the volume of bubbles in 2D should be expressed the same way you express the volume Vf in 2D, i.e., per length dz. I think you should arrive at the same result, since the factor dz vanishes when dividing volumes. Cheers, Michujo. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Dinanath Sharma
Join Date: Aug 2013
Location: India
Posts: 10
Rep Power: 12  |
When I calculate Vi/Vf for the 3-d case, Vi is pi*D^3/6 since its a bubble and Vf is dx*dy*dz,
So there is no cancellation of 'dz' in the ratio. For the 2-d case If you are asking me to use (pi*D^2/4)/(dx*dy) [Only division of areas], I'll try using that. But the problem I have is with the 3-d case. So, using these relations if I have to find (Vi/Vf)3d / (Vi/Vf)2d, it is not =1 It is in fact (2*D/3*dz) and since dz is much larger than D, the 2-d and 3-d forcing terms won't be of the same order. Please let me know if it is not clear, I'll try to explain in further detail. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi,
If I have understood it correctly, Vi refers to the total volume of bubbles in your control volume, right? Then, 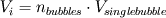 , with , with 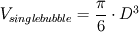 and and 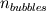 the number of bubbles in the control volume. the number of bubbles in the control volume.In 2D, the number of bubbles in your slice would be 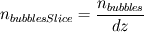 . .On the other hand, the volume of the 2D slice is 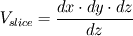 . .The volume ratio is 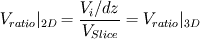 , since the dz factor vanishes. , since the dz factor vanishes.Sorry for the long post. I am just proposing the exact same thing as before, the void fraction is the same in 2D and 3D. Are you using an Eulerian framework for the discrete phase? Cheers, Michujo. |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Dinanath Sharma
Join Date: Aug 2013
Location: India
Posts: 10
Rep Power: 12  |
No, I'm using lagrangian tracking for the dispersed phase.
|
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi,
Is this the paper from which you took the expression for the source term? http://oatao.univ-toulouse.fr/2731/2/Climent_2731.pdf I do not understand what are you referring to with Vf. Is it the volume of the whole domain? Of the cell? Can you please clarify what do you expect to obtain? I do not see why would the force acting upon the bubbles depend on the choice of a 2D or 3D configuration. Cheers, Michujo. |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Dinanath Sharma
Join Date: Aug 2013
Location: India
Posts: 10
Rep Power: 12  |
Hi,
The paper that you have attached uses one-way coupling. (No effect of the bubble motion on the surrounding fluid). I am using 2-way coupling, where there is a source term generated due to the motion of the bubbles in the momentum eqn of the continuous phase. The source term was borrowed from this paper: http://scitation.aip.org/content/aip...1063/1.1566754 Vf is the volume of the cell that contains the bubbles. (Not the domain). For 3-d, Vf=dx*dy*dz and for 2-d it is simply dx*dy (If we are simply using areas for the ratio).. For 2-d Vi is pi*D^2/4 where as from 3-d it is pi*D^3/6. |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 15  |
Hi, thanks for the link. I could not access it by a found another reference where the same expression is used:
http://www.lmm.jussieu.fr/~zaleski/Papers/tomar-CAF.pdf First of all: Do we agree that the results should be the same in 2D or 3D assuming the real flow is really 2D? If yes => I woult not use the area relation, as that would imply that you are assuming cylindrical particles along the z axis, rather than spherical. As I understand it, a 2D approach means that the solution is uniform along the z axis. Now, being the particles spherical, that would mean that, along the z axis, you would have a string of particles located at a constant distance one behind the previous one. Let's say that, in 3D, in the dx*dy*dz cell you have Nbubbles=Nx*Nx*Nz bubbles distributed uniformly, so that the volume ratio in the cell would be 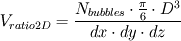 . .In a 2D slice with dimensions dx*dy*1, the number of bubbles would be Nbubbles=Nx*Nx*Nz/dz (and yes! you could come up with a non-integer number of bubbles here!). The initial Nbubbles in 3D is something you need to define (or equivalently, the concentration of bubbles along the z axis). Does it make sense? What do you think? Cheers, Michujo. |
|
|
|

|
|
 |
| Tags |
| coupling, lagrangian particles, two-phase flow, two-way |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| momentum source term | zwdi | FLUENT | 14 | June 27, 2017 15:40 |
| coupling vof with single phase flow and gravity term | alame005 | Main CFD Forum | 7 | August 6, 2013 11:02 |
| [swak4Foam] funkySetFields compilation error | tayo | OpenFOAM Community Contributions | 39 | December 3, 2012 05:18 |
| Plasma Flow Modelling using Source term and cell's data | Constantine | Fluent UDF and Scheme Programming | 2 | May 19, 2010 21:06 |
| Source term in two-phase flow | chouki | FLUENT | 0 | February 15, 2008 07:55 |