 |
|
|
[Sponsors] | |||||
Outflow boundary condition in cartesian grid SIMPLE velocity-pressure coupling |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Gustavo
Join Date: Jun 2013
Posts: 26
Rep Power: 13  |
Hello,
I am writing a code to solve the full incompressible Navier-Stokes equations on cartesian uniform staggered grid. The code pretty much follows Patankar's book. However, I haven't been able to figure out the boundary conditions for a simple bidimensional parallel plate flow. For now, I want to specify the inlet boundary condition as prescribed velocity. In order to do that, I have created virtual volumes in the inlet to specify the velocity. The no-slip boundary condition on the walls also seem to work just fine using virtual volumes. Therefore, I am thinking that the problem may be in the outflow boundary condition. The outflow boundary condition I am applying right now is making the outlet velocities (both u and v) equal to the adjacent west volume so that the gradient with respect to x is zero on the outlet. However, I am unsure whether or not I should apply any boundary condition in the pressure correction equation. So far, I am setting the pressure correction to zero in a single element, either in the inlet or in the outlet, so that I have a reference pressure. The remaining pressure field was supposed to adjust to the flow. I am also unsure on how I should correct the velocities, especially the outlet ones, as they were calculated equal to their adjacent west node so that there is no 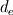 or or 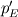 to correct them. So far, I am making them equal to their corrected west velocities as well. to correct them. So far, I am making them equal to their corrected west velocities as well.Right now, my code run and converges, but not to the correct solution. Furthermore, the solution is completely different depending on where my reference pressure is. For example, the velocity-u map below is the converged solution when the reference pressure is in the outlet:  However, if the reference pressure is set in the inlet, the following u-velocity is the converged result:  Furthermore, the result is also very mesh-sensitive. As the mesh gets finer and finer, the velocity profile tends to uniformity (to inlet velocity, if ref. pressure is set in the outlet, or to zero, if ref. pressure is set in the inlet). Furthermore, the resultant pressure field is higher in the outlet than in the inlet if the reference pressure is set in the outlet and lower in the outlet than in the inlet if the pressure is set in the inlet. Furthermore, the delta p increases as the mesh gets finer. The Reynolds number of this problem is about 100 based on hydraulic diameter, in the inlet u = 1 v = 0. I have been dealing with this problem for the last entire month and have not been able to find any mistake. I am doing pretty much what's been described in most CFD books I could reach (Vergeer's, Patankar's, Maliska's, Tennehill's, Anderson's and several documents I found around the web), but I have no idea why the code is not working, though I believe it might because of faulty boundary conditions. I have gone through all my matrixes and I have redone my code by hand several times to check if I was missing something, but I couldn't find an error. I am using MATLAB to implement the code and am creating a sparse matrix with the coefficients. The linear system of equations is solved by MATLAB's default matrix inversion technique by using A\b. Perhaps if I was pointed to a code solving a similar problem using a similar method I could also figure out what I am doing wrong. Thanks for your patience so far! Any suggestion is highly welcome! Last edited by ghobold; April 29, 2014 at 22:53. Reason: S |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Gustavo
Join Date: Jun 2013
Posts: 26
Rep Power: 13  |
I just noticed something interesting. If, for example, I set the reference pressure in the middle cell of my domain (N/2, M/2), then the flow stops right where the reference pressure is set. So it seems like wherever I set the reference pressure, the flow stops right there.
If I do not set any reference pressure, the code does not converge. Refer to the image below:  Figure showing what happens if pressure reference is set at (N/2, M/2)  Figure showing what happens if pressure reference is set at (N/2-N/4, M/2-M/4) Any ideas on what may be causing this problem? |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Troy Snyder
Join Date: Jul 2009
Location: Akron, OH
Posts: 219
Rep Power: 19  |
Is this flow between parallel plates?
If so, I would suggest explicit setting of pressures at both the inlet and outlet. The velocities can then be extrapolated from the interior to the boundaries. In regard to the pressure correction equation, the pressure corrections would remain zero at the inlet and outlet and extrapolated from the interior to the solid walls. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Gustavo
Join Date: Jun 2013
Posts: 26
Rep Power: 13  |
Dear tas38, thanks for your input
The flow is between parallel plates. I just tried to set the inlet and outlet pressure (although I have tried that before). However, pretty much the same thing happened. The flow has the same behavior as in the first figure in the first post. One thing actually bothers me when setting the inlet and outlet pressure, though. Why should the code interpret that the flow is coming from a free stream and into the plates (developing flow) and not interpret it as a fully developed flow? I will now test the lid-driven cavity flow to see if the problem is really the inlet/outlet boundary conditions or if it is something else internal. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Gustavo
Join Date: Jun 2013
Posts: 26
Rep Power: 13  |
Ok, I am starting to think the problem might not be the boundary conditions, but the code itself. Here are the u-velocity contours for the lid-drive cavity problem:
 Does any one have any idea of what could be causing this problem? I have a few thoughts about what could be: 1) the velocity-correction equations: I am having some trouble understanding how to correct the velocities in the SIMPLE scheme. For example: if I am using ghost cells to define no-slip conditions, say, for x-velocity on the upper plate (by making 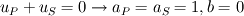 ), then how should I correct the velocity on the ghost cell? Does it have to be corrected? ), then how should I correct the velocity on the ghost cell? Does it have to be corrected?2) The pressure-correction equation: What are those 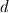 coefficients? I am not sure I am using them correctly. coefficients? I am not sure I am using them correctly.3) Calculating the coefficients: The way Patankar's (and others) book describe the generalized discretization assumes the continuity equation is satisfied. But it is not before convergence. Is that a problem? Thanks |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Gustavo
Join Date: Jun 2013
Posts: 26
Rep Power: 13  |
I'm still stuck with this problem. Anyone's got any idea?
Thanks! |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Troy Snyder
Join Date: Jul 2009
Location: Akron, OH
Posts: 219
Rep Power: 19  |
Can you post the code?
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
Gustavo
Join Date: Jun 2013
Posts: 26
Rep Power: 13  |
Hello tas38,
You can find my code in the following link: https://www.dropbox.com/sh/wnhidgmg6...aQTfmL34nuP9Ka The code is organized as follows: testNS.m initializes the problem and plots the solution solveNS.m calls for momentum and continuity solvers and corrects velocities and pressure solveXMomentum.m solves the x-momentum equation solveXMomentum.m solves the y-momentum equation solveContinuity.m solves the pressure correction equation residual.m calculates the residual for momentum equations B.m is the interpolation function (power law) staggeredToNodeU.m transforms the staggered U values into co-located values (only used to plot the results) Thanks for your willingness to take a look at my code, I hope it's understandable! |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Parth Thaker
Join Date: Mar 2014
Location: Surat , Gujarat , INDIA
Posts: 26
Rep Power: 12  |
if ur code is semi-explicit , give time step very very near to stability criteria, looking at ur lid driven result it seems ur using very small time step,if code is implicit i got no clue . . .
|
|
|
|

|
|
|
|
|
#10 |
|
New Member
Adim
Join Date: Sep 2015
Posts: 1
Rep Power: 0  |
did you find out how the outflow boundary condition must be handled?
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure boundary condition | C-H Kuo | Main CFD Forum | 18 | September 16, 2016 03:19 |
| LES in DES can't be actived! | shenying0710 | CFX | 17 | January 23, 2014 04:45 |
| Question about heat transfer coefficient setting for CFX | Anna Tian | CFX | 1 | June 16, 2013 06:28 |
| Velocity profile boundary condition | Tuca | FLOW-3D | 1 | April 23, 2013 12:02 |
| Pressure Boundary Condition | Matt Umbel | Main CFD Forum | 0 | January 11, 2002 10:06 |