 |
|
|
[Sponsors] | |||||
coefficient calculation (a_P, a_nb) in unstructured meshes vs. structured meshes(FVM) |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 206
Rep Power: 16  |
I am currently trying to understand unstructured meshes and am implementing the diffusion equation on a simple 2D rectangular domain with an unstructured mesh. I did this a while back for structured meshes and I was calculating the neighbor coefficient as
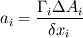 where 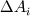 and and 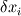 are the cross sectional area (per unit lenght) and the distance of two neighbor cells (cell center to cell center). The cross sectional area is simple are the cross sectional area (per unit lenght) and the distance of two neighbor cells (cell center to cell center). The cross sectional area is simple 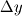 in the x direction and in the x direction and 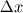 in the y direction. in the y direction.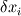 is defined is defined 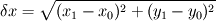 . . The index 0 refers to the current cell and 1 to one of its neighbor. 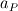 for each cell in turn is then calculated as the sum for each cell in turn is then calculated as the sum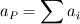 Hence, if  is positive, all is positive, all 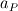 and and  must be positive for each cell as each component is positively defined (i defined must be positive for each cell as each component is positively defined (i defined 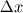 and and 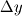 positive for each cell). positive for each cell). For unstructured meshes, the neighbor coefficients are calculated as 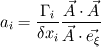 where 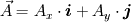 and 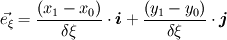 . .If I expand 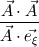 I get I get 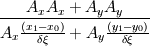 Since both 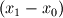 and and 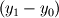 can take negative values, it is expected that both can take negative values, it is expected that both 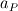 and and  can take negative values. can take negative values. Now I am not sure if that is to be expected (as for the structured code I get solely positive values) but I am having the feeling that this i causing some problems for my code. So the question is probably more, is there any definition for face/unit vector of 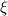 for the direction they are pointing? Not sure if that is the only problem that I am having in the code, but at least its the only one I can identify to be not working at the moment. The gradient calculation seems to give physical results and I have tried to solve with and without the secondary gradient (cross diffusion term) to check if the error is coming from this term but it does not seem so. for the direction they are pointing? Not sure if that is the only problem that I am having in the code, but at least its the only one I can identify to be not working at the moment. The gradient calculation seems to give physical results and I have tried to solve with and without the secondary gradient (cross diffusion term) to check if the error is coming from this term but it does not seem so. I am using a face based approach where I solve over each face in the interior (followed by the boundary faces) where I add contribution to cell 0 (current cell I am in) and substract them from cell C1 (neighbor cell). If anyone with experience with unstructured meshes and has a hunch what I am doing wrong I would appreciate the help. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Quote:
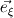 will be pointing in *almost* the same direction as will be pointing in *almost* the same direction as 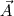 and the dot products will all be positive. In the limit of no grid skewness, they will be parallel and you will get the same expressions you had for your structured Cartesian code. and the dot products will all be positive. In the limit of no grid skewness, they will be parallel and you will get the same expressions you had for your structured Cartesian code.Remember that the coefficients you are computing are really just approximating the summation of the gradient of the unknown quantity at the face dotted with the face area vector. The direction of the area vector assumes that flux is exiting cell0 and entering cell1. Here is how it is done in ANSYS Fluent for reference--note Figure 3.2.2: http://aerojet.engr.ucdavis.edu/flue...udf/node92.htm |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 206
Rep Power: 16  |
thanks, my area and unit vector where in fact pointing in different directions for some cells, problem is solved now and results look as expected. my cross diffusion term is making something odd but without it its ok. will try to track that bug down. but thanks again.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| structured and unstructured grids | user | Main CFD Forum | 6 | November 25, 2010 01:14 |
| structured or unstructured??????? | vijesh joshi | Main CFD Forum | 1 | May 9, 2006 12:16 |
| Structure vs unstructured meshes | Des Aubery | Main CFD Forum | 2 | July 25, 2003 23:11 |
| Higher Order FV Schemes for unstructured meshes | Apurva Shukla | Main CFD Forum | 4 | December 15, 2000 09:17 |
| unstructured vs. structured grids | Frank Muldoon | Main CFD Forum | 1 | January 5, 1999 10:09 |