 |
|
|
[Sponsors] | |||||
Non orthogonal correction for diffusion-like term in pressure equation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 11  |
I am having trouble deriving the discretized form of the pressure equation for a collocated variable arrangement on unstructured grids using a finite volume method as it is presented in
Code:
@article{darwish09,
title = "A coupled finite volume solver for the solution of incompressible flows on unstructured grids ",
journal = "Journal of Computational Physics ",
year = "2009"
}
@article{mangani14,
author = {Mangani, L. and Buchmayr, M. and Darwish, M.},
title = {Development of a Novel Fully Coupled Solver in OpenFOAM: Steady-State Incompressible Turbulent Flows in Rotational Reference Frames},
journal = {Numerical Heat Transfer, Part B: Fundamentals},
year = {2014},
}
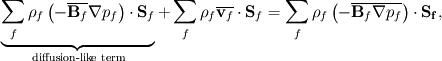 where 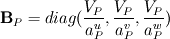 and the overline denotes linear interpolation between values of the neighboring cells and the overline denotes linear interpolation between values of the neighboring cells  and and  . I am interested in the discretization of the term with the underbrace. . I am interested in the discretization of the term with the underbrace. Normally one would assume 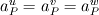 and proceed without problems, but there are situations in which this is assumption is incorrect, for example if different under relaxation factors are used for the different momentum balances or, which is why I am interested in this, a problem is solved involving wall boundaries. and proceed without problems, but there are situations in which this is assumption is incorrect, for example if different under relaxation factors are used for the different momentum balances or, which is why I am interested in this, a problem is solved involving wall boundaries.I am aware that for wall boundaries there exist discretizations that avoid the formulation of different diagonal contributions for each momentum balance, but I think a fully coupled solution approach should take this into account. Problems surge, when I try to discretize the diffusion-like operator from the pressure equation. Normally those terms are discretized as 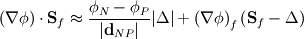 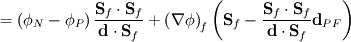 using the "over-relaxed" correction approach (s.a. Jasak's Phd Thesis). What I can't understand is the derivation of the discretization for the pressure equation, since it involves an additional (diagonalized) operator, 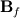 . Can someone explain how to derive the result presented in the above mentioned paper: . Can someone explain how to derive the result presented in the above mentioned paper: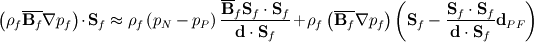
|
|
|
|

|
|
 |
| Tags |
| discretization, non orthogonal |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Non-linearity Pressure Equation -- PISO algorithm | gdeneyer | OpenFOAM Programming & Development | 1 | August 23, 2012 05:19 |
| Timestep and Pressure Correction Relationship in SIMPLE | rks171 | Main CFD Forum | 23 | May 4, 2012 01:04 |
| changing the coefficients of pressure correction | Noel | Phoenics | 1 | April 7, 2009 08:54 |
| BCs for Pressure Correction Equation (SIMPLE) | Bharath Somayaji | Main CFD Forum | 1 | March 1, 2006 06:12 |
| Preconditioning for Pressure Correction Equation | cfd101 | Main CFD Forum | 1 | February 23, 2006 14:34 |