 |
|
|
[Sponsors] | |||||
[3D Vortex Particle Method]The function in diffusion operator |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Youjiang Wang
Join Date: Apr 2015
Location: Hamburg
Posts: 22
Rep Power: 11  |
For the vorticity diffusion, the Laplacian operator
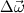 is always replaced by an integral operator is always replaced by an integral operator  . A function . A function 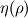 is used in the integral. Then the diffusion term looks like is used in the integral. Then the diffusion term looks like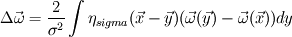 and 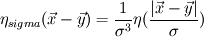 ,for the vortex particle method, the change of particles' strength according to the diffusion would be ,for the vortex particle method, the change of particles' strength according to the diffusion would be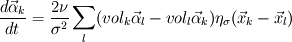 It is said that the function 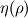 can be got from the vorticity smoothing function can be got from the vorticity smoothing function 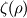 as as 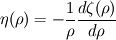 My question is that, there is a 2nd order algebraic smoothing function 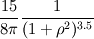 and a 4th order Gaussian smoothing function and a 4th order Gaussian smoothing function 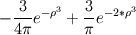 . I have calculated the corresponding integral function for the both smoothing functions, and plotted against . I have calculated the corresponding integral function for the both smoothing functions, and plotted against  . However, as i see it, the properties are really different . However, as i see it, the properties are really different  . . tmp.jpg Which is correct? Or both can be used?  
Last edited by wyj216; April 20, 2015 at 04:39. Reason: correct notation errors and make it more clear |
|
|
|

|
|
|
|
|
#2 |
|
Member
Join Date: Jul 2013
Posts: 56
Rep Power: 12  |
1) Two small comments on notation. It might be a personal preference more than a requirement, but still.
a)2) I have not yet worked an applied project with vortex formulation, but the two function plot made me think about classic results from Lamb-Oseen (Vorticity distribution and Velocity distribution). Your 2nd order algebraic looks like it's more or less the cylindrical derivative about r or your 4th order Gaussian. I might be wrong, but maybe you have mixed some things you shouldn't mix. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Youjiang Wang
Join Date: Apr 2015
Location: Hamburg
Posts: 22
Rep Power: 11  |
Quote:
I have just began to do some testing code for the 3D particle method. Thus i'm not clear with some concept and equations. Sometimes my question may seem to be quite strange, and i'm sorry for that. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Serguei
Join Date: Mar 2015
Posts: 33
Rep Power: 11  |
First of all, forget for the moment about math and diffusion also. What is the vortex particle in your model for the 3-d? So, I mean, what is the vorticity "atom", or the singular element physically?
|
|
|
|

|
|
|
|
|
#5 | |
|
New Member
Youjiang Wang
Join Date: Apr 2015
Location: Hamburg
Posts: 22
Rep Power: 11  |
Quote:
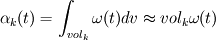 And the position of the particle 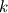 is the position of the initial vorticity at time is the position of the initial vorticity at time 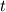 . So it's a Lagrangian description of the vorticity field. . So it's a Lagrangian description of the vorticity field.
|
||
|
|

|
||
|
|
|
#6 |
|
Member
Serguei
Join Date: Mar 2015
Posts: 33
Rep Power: 11  |
Actually, there two way to describe the vorticity fields: contentious and discrete. When you are talking about particles "atoms", you assume some discrete set of the elements, which induct the VELOCITY NOT THE VORTICITY between themselves and interact with each other. That is it. After understanding that, you should start to think about nature of those vorticity particles "atoms". For 2-d, that is easy. They are just points, or some pieces of distributed by some way vorticity inside. (Inside each of them, not outside !). They are strait and infinite in the perpendicular direction. For 3-d everything become much complicate on this stage. The vorticity lines should either go to infinity or be closed. Each of those way of representation is a very challenging.
|
|
|
|

|
|
 |
| Tags |
| 3d vortex particle method, diffusion, smoothing function |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [snappyHexMesh] How to define to right point for locationInMesh | Mirage12 | OpenFOAM Meshing & Mesh Conversion | 7 | March 13, 2016 14:07 |
| Error during reconstructing lagarangian fields | ybapat | OpenFOAM | 9 | November 17, 2014 07:52 |
| injection problem | Mark New | FLUENT | 0 | August 4, 2013 01:30 |
| [swak4Foam] installation problem with version 0.2.3 | Claudio87 | OpenFOAM Community Contributions | 9 | May 8, 2013 10:20 |
| [blockMesh] non-orthogonal faces and incorrect orientation? | nennbs | OpenFOAM Meshing & Mesh Conversion | 7 | April 17, 2013 05:42 |