 |
|
|
[Sponsors] | |||||
Generating elliptic grid around NACA SC2-0714 airfoil |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
I'm attempting to generate an elliptical grid around the said airfoil. Please keep in mind I'm a newbie to CFD so if you could keep responses as simple as possible, I'd super appreciate it! I'm using MATLAB for generating the grid and other calculations. I have several questions though. From what I'm told, it's reasonable to have the grid extend out in all directions roughly fifteen times the chord length. Attached is a plot of the airfoil shifted on the x-axis in order to make room for the elliptic grid. The plot was generated via coordinates found online. Where I'm having trouble is actually generating the grid by only knowing the coordinates of the airfoil.
What I know is that I'll have a predetermined number of grid points in both the where 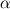 , , 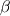 , and , and 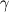 , there are no x or y at grid point i,j...so I'll spare myself typing the finite difference representations. So, solving the first two equations in their finite difference equivalents at point i,j we get , there are no x or y at grid point i,j...so I'll spare myself typing the finite difference representations. So, solving the first two equations in their finite difference equivalents at point i,j we getI also know I'll be using a loop to determine each x and y at point i,j and terminate the loop once the above differences have converged on a point. I'm just not sure about what to do next. How do I generate the elliptical grid by only knowing the x and y values of the airfoil? I've Googled many different things, searched this forum itself, tried using the Joe Thompson book on grid generation on Mississippi State University's website, none of which have truly helped. Any advice is greatly appreciated. I'm not looking for an outright answer...but rather where to look or some hints. I feel like I'm close but being that this is my first endeavor with grid generation, it's pretty tough. Last edited by DA6righthand; June 27, 2015 at 11:23. |
|
|
|

|
|
|
|
|
#2 |
|
Member
A. S.
Join Date: Apr 2009
Location: Raipur (INDIA)
Posts: 54
Rep Power: 17  |
Hi
First you have make grid using Transfinite Interpolation, between airfoil and outer domain. Then you have to fix the boundary vertices and march with elliptic grid generation method to get better grid. Also recheck the formulation of finite difference you are using more specifically the last term. It should be i,j+1 - i,j-1 if I remember correctly. If you need further help drop me a message. Regards Apoorv |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
Quote:
I'll look up transfinite interpolation and see if I get anywhere. I appreciate it! |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
As said by apoorv, in order to run an elliptic solver you need to prescribe both inner and outer boundaries and provide an initial "guess" for the interior nodes. The need for an accurate initial guess will strongly depend on the robustness of your elliptic solver but usually transfinite interpolation is necessary.
On the other side, hyperbolic mesh generation does not need information coming from the interior (thanks to the hyperbolicity) thus the algorithm generates successive layers from the only information coming from the airfoil coordinates (note that in this case it is difficult to get control on outer boundary node distribution). Though ,this method naturally imposes orthogonality and is order of magnitude faster computationaly. Look for Sorensen technical paper if interested |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
I've done a bit of reading on transfinite interpolation and from what I understand is that I need a set of curves in order to set up the interpolation equation. Suppose I enclose the airfoil with a basic circle. Then I'd have curves enclosing the airfoil on the top and bottom...but how to I account for the airfoil in the center of the circle? Every internet resource I've looked seems to indicate that transfinite interpolation needs four curves enclosing the domain: top, bottom, left, and right.
I read the Thompson grid generation book sections on Lagrange and transfinite interpolation and his notation is a little confusing/hard to read but I think I'm understanding it a bit better. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
You are right you need a set of four curves, but this is also what you need for your elliptic solver. The definition of these four boundaries will define the type of grid you are constructing, have a look to C-grid, O-grid and H-grid
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
I figured I'd let you know how I generated my grid. I searched about transfinite interpolation and couldn't figure it out. So here's what I did. I have the coordinates of the airfoil and the circle enclosing it. So between each coordinate of the airfoil and circle, starting from the trailing edge of the airfoil and 0*pi, I created a predetermined amount of linearly spaced x-values and used linear interpolation to find each new y coordinate. It worked just fine, as did generating the elliptic grid.
The only issue I'm having now is the amount of time it takes to generate the elliptic grid. Right now, with 42025 i,j points it takes 4 hour and 50 minutes to form the elliptic grid. Currently I'm using a while loop with two for loops within it. The for loops solve the finite difference equations in my first post for the elliptic grid. The while loop keeps iterating the for loops until the error between the x or y coordinate matrices reach a certain level (set at 0.00001). The way I'm evaluating the error is the Frobenius norm. For example, the error for the x matrix is The error decreases very slow. Is there a more efficient way to evaluate error? Should I use a different norm to evaluate error? I'm looking for anything to speed up generating the grid. If anyone wants to see my code just let me know...I'll post it. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
I'll help you figure out how to implement transfinite interpolation, I did it some time ago, just need to find the code.
About tolerance, I do not see a critical problem, maybe I would have taken the Linfinity norm or would have scaled your actual norm by the total number of nodes. Anyway, if your solver is slow it is likely due to the way you solve the discrete equations. Could you post your code ? Cheers |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Hi, I found the routine I used to compute TFI as an initial guess for the elliptic solver.
As for the elliptic solver itself, here is the sequence I used: - TFI - elliptic solver without forcing terms - elliptic solver + forcing terms I solved the discrete equations using Multigrid + gauss-seidel (I am not saying it is the best option though, but computational time was acceptable, but still magnitude slower than the hyperbolic solver however) |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
naffrancois, thanks for your replies. Here is what I did in MATLAB (the only way I can fluently code). Between each point on the airfoil and enclosing circle I designated a set amount of x values linearly spaced apart. Then I used simple linear interpolation to find the y values. This generated an algebraic grid but when I run my elliptic solver, the elliptic grid is not reasonable. In other words, the elliptic grid looks good at the leading edge (sufficiently dense grid points) but the trailing edge of the airfoil is not dense enough. If you're able to run MATLAB files, attach is my code. If you cannot run MATLAB, here is my code below.
I'm working on another code also. The limitation to my attached code is that it is limited to a set number of grid points. The .txt file containing the airfoil coordinates has 205 x-values and 205 y-values. The way I wrote my code is the enclosing circle will have 205 x-value and 205 y-values. Conveniently, the airfoil coordinates begin at the trailing edge and progress counterclockwise around the airfoil. I generated the circle in the same manner beginning at 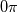 and ending and ending 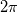 . That way when generating the algebraic grid, it begins at the trailing edge of the airfoil and the point at . That way when generating the algebraic grid, it begins at the trailing edge of the airfoil and the point at 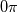 and increments counterclockwise. and increments counterclockwise. I'm just not entirely sure how to write a code that allows for an alternate number of grid points. I though about using several MATLAB builtin functions such as polyfit and polyval to generate a polynomial that fits the airfoil. This would allow any x and y in the domain of the airfoil to be evaluated. Although, doing so would introduce some amount of error. I experimented with the polyfit functions and was able to produce polynomials that very closely fit the original airfoil. In order to do this, I had to make two polynomials to represent the airfoil: one to plot the top half of the airfoil, the other to represent the bottom of the airfoil. MATLAB tells me that the polynomials are "poorly conditioned" though because I had to use polynomials of high degree (degree 19 for the top of airfoil, 20 for the bottom of airfoil). Other than what I described, I had no idea how to write a code that allows for an alternate number of grid points. My current code generates 205 by 205 x and y matrices. That yields 42025 grid points. I imagine I'll want more grid points when performing calculations for compressible supersonic flow. Code: function AirfoilTrans B=load('NASASC20714AirfoilCoordinatesSelig.txt'); x1=B(1:end,1); y1=B(1:end,2); %center airfoil at the origin for i=1:length(x1) x1(i) = x1(i) - 0.5;end R=5; L=length(y1); theta=linspace(0,2*pi,L); x2=R*cos(theta); y2=R*sin(theta); % figure(1) % plot(x1,y1,x2,y2) x=zeros(L,L); y=x; z=y; for i=1:L x(i,1)=x1(i);end %Create algebraic grid by linearly spaced elements between known x %coordinates on airfoil and circle then linearly interpolate to find values %of y for i=1:L deltaX=linspace(x(i,1),x(i,end),L);end figure(1) surf(x,y,z) errX=1; errY=1; err = 0.00001; xold=x; yold=y; xi=linspace(0,1,L); dxi=xi(2)-xi(1); eta=linspace(1,abs(R/max(y1)),L); deta=eta(2)-eta(1); iter=0; while errX > err || errY > err end figure(2) surf(x,y,z) |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Hello, sorry for the late reply, I am pretty busy at the moment and will give you a more complete answer in the coming days.
About node distribution, you are right, you should have two distinct node distributions, one describing the geometry (the input coordinates describing the airfoil) and your mesh boundaries. Have a look to cubic splines interpolation. It does not try to fit a single polynomial to the whole set of airfoil coordinates, instead it builds piecewise cubic polynomials between each nodes. You could also try simple linear interpolation between each airfoil coordinate nodes at first, but keeping in mind that the error will be high |
|
|
|

|
|
|
|
|
#12 |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
Linear interpolation is kind of what I did. I placed a certain amount of x values between each coordinate on the airfoil and circle, then used basic linear interpolation to determine the y coordinates of the algebraic grid.
So you think a spline would work better the fitting a high degree polynomial to the airfoil? I'll try this later today and see what happens. Thanks! |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
I think we misunderstood each other, if not excuse me if you already understood the following. About linear interpolation or cubic splines, I was talking about how you could get any number of nodes on j=1 line (on your airfoil then).
For now, the code you gave me (which runs well by the way), allows for exactly the same number of nodes on j=1 (and as a consequence on j=jmax) than the number of coordinates you give in input. In order to allow for a more flexible mesh generation, the first step in to interpolate the input coordinates of your airfoil to a new set of nodes (on j=1). I believe that you cannot fit these coordinates by a single polynomial, instead either you can have a look at cubic splines, or can try to simply linearly interpolate between each airfoil coordinates (but you may have surprises when running later your CFD code on it). Then, you have an independent j=1 node distribution and you can go for the generation of the interior mesh: - algebraic initial guess (linear interpolation as you did is ok for your configuration because the convexity of your airfoil is not very high, or more robust guesses like TFI) - elliptic smoothing Then, you will have a look at forcing terms to enforce grid stretching and orthogonality. |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
About speed of the elliptic solver, one thing you should look at is the initial guess (algebraic grid). If you zoom close to the trailing edge, you will see crossing lines, in my opinion this may affect the rate of convergence badly
|
|
|
|

|
|
|
|
|
#15 |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
About the trailing edge of the airfoil: I was told it might help to slightly alter the very last few coordinates of the airfoil and this could help.
If you ran my code, you'll see the elliptic grid is fairly condense at the leading edge while the trailing edge is not. Do forcing functions help control the grid density or is the problem arising from the algebraic grid? I really appreciate all of your help, by the way. Thanks! |
|
|
|

|
|
|
|
|
#16 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
I am not refering to the coordinates of the trailing edge, but to the algebraic grid shown in figure(1) of your matlab code, if you zoom near the trailing edge, right below you will see that lines are crossing each other. This might be problematic and slow down the elliptic solver.
About grid density, you are right, forcing functions will help a lot in clustering nodes where you want or impose orthogonality to the airfoil. |
|
|
|

|
|
|
|
|
#17 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Here are some pictures of results of applying different approaches I did some time ago:
- TFI - Laplace - Laplace + forcing functions - Hyperbolic As you see, the TFI and Laplace without forcing terms give a poor quality grid. The reason is that they do not have any mechanism to enforce orthogonality and much control on the interior grid spacing. With forcing functions you can force the grid to some extend I think I took as a reference the source codes coming with the book of Blazek: - Computational fluids dynamics: principles and applications grid_TFI.jpg grid_Laplace.jpg grid_Poisson.jpg grid_Hyperboic.jpg |
|
|
|

|
|
|
|
|
#18 | |
|
New Member
Justin
Join Date: Jan 2015
Posts: 28
Rep Power: 11  |
Quote:
where 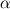 , , 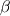 , and , and 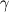 are as defined in the original post, are as defined in the original post, 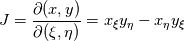 is the Jacobian, and P and Q are given by is the Jacobian, and P and Q are given byIn P and Q, n is the number of 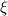 lines and m is the number of lines and m is the number of 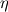 lines. The amplification factors are lines. The amplification factors are 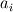 and and 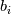 . According to the Chung book, . According to the Chung book,-So should I choose distinct amplification factors for each point? Or could I just make it a constant? Basically my goal now is to condense the 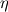 lines closer to the airfoil and condense lines closer to the airfoil and condense 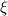 lines closer around the leading and trailing edges. But, being a newbie to CFD, I'm not sure how to manipulate these forcing functions. Although it seems the only way to enhance my current elliptic grid is by using these forcing functions. lines closer around the leading and trailing edges. But, being a newbie to CFD, I'm not sure how to manipulate these forcing functions. Although it seems the only way to enhance my current elliptic grid is by using these forcing functions.My question is when I write the finite difference form with the forcing functions, will I have to sum to n and m for each iteration (i.e. for each i,j)? I'm a little confused on how to incorporate that into the differenced equations. Last edited by DA6righthand; July 21, 2015 at 19:22. Reason: clicked submit reply rather than preview reply...I stoopid |
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Hello, I did not use these forcing functions, I think I used the one based on orthogonality properties (it is mentionned in the book of Chung). Nevertheless, in order to test them, you should probably focus first on clustering at a single location. The first term clusters lines and the second term clusters towards points. You should try first to cluster only to eta=1 line rather than setting different clustering locations, as you will see you rapidly get an unstable solver.
Looking at the expressions for P and Q, it seems that you can precompute these quantities before the solving step, no need to recompute them as they do not depend on physical points. Would not be a bad idea to test it on a simpler geometry like a square first good luck and let me know ! |
|
|
|

|
|
|
|
|
#20 |
|
Member
mechiebud
Join Date: Jan 2015
Posts: 49
Rep Power: 11  |
Quote:
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| SU2 AOA optimization | 454514566@qq.com | SU2 | 9 | March 7, 2022 16:17 |
| elliptic grid generation (orthogonal) | vasu | Main CFD Forum | 8 | October 28, 2015 15:20 |
| [ICEM] O-grid mesh for NACA airfoil | SR-71 | ANSYS Meshing & Geometry | 0 | February 6, 2015 07:45 |
| 2D FFD Optimization | RLangtry | SU2 | 2 | August 5, 2014 09:48 |
| Structured Airfoil Grid Generator | A.S. | Main CFD Forum | 1 | September 30, 2008 18:29 |