 |
|
|
[Sponsors] | |||||
pressure-based coupled solver for compressible NS equation |
 7Likes
7Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Hi,
I am a CFD hobbyist and am trying to put together a pressure-based coupled solver. The FVM solver is supposed to solve transient compressible flow on tetrahedrons. I am aware of the methods in literature (Chen and Przekwas, Kambrath et al., Darwish et al., etc.), where the problem was manually linearized to construct the Jacobian. However, the Newton-GMRES method (from the SUNDIALS-KINSOL of LLNL) is used in my code. So I have avoided (for now) manually dealing with the nonlinearity or assembling the Jacobian. The nonlinear residual function 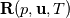 reads (viscous and conduction terms are not shown): reads (viscous and conduction terms are not shown): ![\rho\mathbf{u}-\rho_0\mathbf{u}_0-\frac{dt}{V}\left[\oint_{\partial V}\rho\mathbf{u}(\mathbf{u}\cdot\hat{\mathbf{n}})dA+\oint_{\partial V}-p\hat{\mathbf{n}}dA\right] \rho\mathbf{u}-\rho_0\mathbf{u}_0-\frac{dt}{V}\left[\oint_{\partial V}\rho\mathbf{u}(\mathbf{u}\cdot\hat{\mathbf{n}})dA+\oint_{\partial V}-p\hat{\mathbf{n}}dA\right]](/Forums/vbLatex/img/1723369e5a00f1135b91b74c25660127-1.gif) 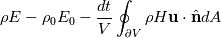 where 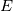 is the mass-specific stagnation internal energy, and is the mass-specific stagnation internal energy, and 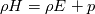 . .Because the FVM configuration is co-located, the 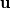 at at 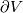 includes an additional Rhie-Chow component. includes an additional Rhie-Chow component.Both 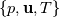 and the residuals are scaled to homogenize their magnitude as suggested by SUNDIALS-KINSOL. and the residuals are scaled to homogenize their magnitude as suggested by SUNDIALS-KINSOL.However, even the brutal force method (numerical dense Jacobian + dense direct solver) fails (reduces the residual by 1-2 orders of magnitude, then stalls). The good news is the non-converged result is not too bad visually. I know that at this point its hard to ask an appropriate question that can lead to any useful answer. But I just want to confirm that this concept of pressure-based coupled solver is not too stupid and has the potential to work. If there is no major problem with such concept, I'll work on estimating the Jacobian and constructing a preconditoner for the GMRES. Otherwise, I'll tried to simplify the non-linear problem thrown to the Newton method by linearizing it. In the case that you really want to get your hands dirty, here is the code: https://github.com/mianzhi/fosolvers and here is how to make it work on your machine: https://drive.google.com/open?id=0B0...ktBSzIwSlRzdk0 I would also be more than willing to send you the grid file and the input file with which I'm tuning the code. I appreciate your time and input. Best regards, Mianzhi |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
So far based on my experience with fluent\s coupled solver, they are able to get good performance because of use of D-ILU preconditioner.
From my own coding experience with coupled solver, the advise that I would give any one is to use continuity convergence accelerator. In this after coupled system is solved, you only solve continuity or pressure to enforce continuity further. This for me was able to get coupled like performce. The main problem with coupled solver I could see is that linear system taking too much time, hence unless the coupled system is significantly faster (3 times or more) I dont see it beating a normal SIMPLE solver. So in the end, the only advantage remaining of coupled solver is its stability. Good luck and please share results when finally you have it all running. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
are you solving an inviscid flow problem? |
||
|
|

|
||
|
|
|
#4 |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Hi, FMDenaro,
It's a viscous problem. I dropped the viscous and conduction terms in the post to make it looks simpler. Best regards, Mianzhi |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Maybe I do not understand your topic but you wrote about the numerical solution of transient flow problem. The equations you wrote represent for me a first order accurate in time explicit discretization (spatial operators are in continuous form). They can be solved sequentially. But I immagine that you work with higher accuracy in time and for each time step you conversely solve for the coupled equations in iterative way. I never worked in the construction of Jacobian-based methods but I am not sure your are checking for the correct residuals by using those equations...maybe I can be wrong... What kind of flow problem are you solving? |
||
|
|

|
||
|
|
|
#6 | |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Quote:
Compared to the segregate solver, the coupled solve all the residual equations simultaneously. Say there are n FVM cells in 3-D, a system of 5*n nonlinear equations is solved every time step. The value of the nonlinear functions naturally become the residual after they are scaled to comfort the SUNDIALS-KINSOL. In the case that the discretized equation is satisfied, the residual should go to zero. The solver should be good for both supersonic and subsonic flow. It should be able do handle acoustic CFL ~ 10, flow CFL ~ 0.5 |
||
|
|

|
||
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
ok, thus your actual computed residuals are the equations you wrote but with all the surface integrals discretized and the flux functions evaluated at time t+dt, right? I suggest to check for the max norm of the residuals and see the spatial location where the error reaches the max. Check for the residuals computed at the boundaries |
||
|
|

|
||
|
|
|
#8 | |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Quote:
That is right; This is actually what I have tried. It seems that the large residual is both in the domain and near the boundary. I'll visualize the residuals and posted them in the next post. |
||
|
|

|
||
|
|
|
#9 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Quick question: Is the convergence better when you choose a small dt?
I haven't used SUNDIALS, but I have worked extensively with Newton methods. I have yet to read about any full-scale CFD application that can use Newton-Krylov or Broyden-type methods without some form of preconditioning. As masterful as the mathematics are in canned solver routines, I think they meet their match with CFD. If you haven't already, you might want to read David Keyes survey of Newtow Krylov schemes -- it covers preconditioner rationales extensively: http://www.cs.odu.edu/~keyes/papers/jfnk.pdf FUN3D has several preconditioners for its Newton Krylov scheme. Some of its documentation might be helpful. |
|
|
|

|
|
|
|
|
#10 | |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Quote:
Thank you for the pointer to the materials. I think adopting a preconditioner is the next logical step for me to make it work. |
||
|
|

|
||
|
|
|
#11 |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Thank you again for the valuable thoughts you have provided.
I've been testing the code with the following problem. The width in z is 1 m long. The initial pressure is like: p0.png And the initial temperature is uniform: T0.png The gas is stationary initially. Presented below is the "convergence-stalled" result. |
|
|
|

|
|
|
|
|
#12 |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
After one time step,
The pressure becomes: p1.png And the low pressure gas is compressed a little bit, while the high pressure gas expands: T1.png 10 time steps later, the compression and expansion propagates to longer distance: p10.png T10.png |
|
|
|

|
|
|
|
|
#14 |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
I've also visualized the residuals.
It seems that the density residual is correlated with the energy residual. At 0.1 ms: r_rho1.png r_rhoE1.png At 1 ms: r_rho10.png r_rhoE10.png I also noticed that the residual is distributed both internally and near the non-slip walls. |
|
|
|

|
|
|
|
|
#15 |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
|
|
|
|

|
|
|
|
|
#16 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I don't want to comment too much about the images that you posted, mostly because I don't want to risk sending you off in the wrong direction. But, one thing that does occur to me is that the normalization of your residuals may be off. Recognize that the zero initial velocity field may not have provided a reasonable normalization of your momentum residual. I can't say that for certain, but I just raise as something to consider.
At the risk of beating a horse, let me also note that one important aspect of even a simple preconditioner is to approximately map the residual back to the solution and, in doing so, at least get the order of magnitude right. Generating residual normalizations based solely on initial conditions, can lead to seriously misleading convergence estimates. And it can also lead to incorrect estimates of the finite difference parameter (epsilon in the Keyes' paper) used to compute the vector-Jacobian product. If that parameter is incorrectly chosen, the Newton step will stall or diverge because of either gross finite difference inaccuracies (epsilon too big) or loss of numerical precision (epsilon too small). |
|
|
|

|
|
|
|
|
#17 | |
|
Member
Mianzhi Wang
Join Date: Jan 2015
Location: Columbus, IN
Posts: 34
Rep Power: 11  |
Quote:
Yes you are right. When using SUNDIALS-KINSOL, one need to supply both unknown scales and residual scales. The finite differencing in the Krylov method relies only on the unknown scales. In my computation, the scales of unknowns are evaluated before each time step. The velocity scale is evaluated based on both velocity and pressure drop, so the initial zero velocity should not be a problem. Also, the pressure and temperature scales consider the velocity as well. (I'm using the "delta form" for the solution vector {dp,du,dT}) As for the residual scales, I'm using constant values (0.1 kg/m^3 for density, 1 kg/s/m^2 for momentum, 1e4 J/m^3 for energy). Strangely, I need to explicitly code the scaling of the residuals in my nonlinear function, instead of providing the scales to KINSOL as it should be. With the later method the residual just doesn't converge at all. I've actually reported this to the SUNDIALS developer, but there hasn't been a solution/explanation since I've found the workaround for my previous problem. http://sundials.2283335.n4.nabble.co...td4653756.html I've also reviewed the algorithm that KINSOL generates the size of the finite differencing disturbance. It seems that with my current unknown scales, the disturbance should be adequate but not too large. BTW, I've just found a trick to cut the residual (when iteration stalls) to, approximately, half: I took the density residual, multiplied it by E, and subtracted it from the energy residual. I'll start working on the preconditioners and hope the residual can be further reduced. Thank you very much for your input. Wish you have a great weekend. Best regards, Mianzhi |
||
|
|

|
||
|
|
|
#18 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I did have another thought. What interpolation/limiter scheme are you using for your convection terms? If are you are using a non-differentiable limiter for the flux/gradient computation, then you may be experiencing so-called limiter chatter where the solution oscillates between limiter states and fails to converge. Newton methods generally behave poorly when exposed to that kind of non-differentiable behavior, while (pseudo-)transient methods can some times work in spite of it.
If you are using a non-differentiable limiter, you would do well to read up on some limiters that have been developed specifically to be differentiable and provide improved convergence for Newton solvers: http://tetra.mech.ubc.ca/ANSLab/publ...chalak2008.pdf |
|
|
|

|
|
|
|
|
#19 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Actually last few days I have also investigated pressure based coupled solver and the issue of residual stall. My conclusion (just take it as random guys opinion on Internet) on this issue was that the pressure gradient term in coupled system causes most of the convergence problem for coupled system. The way I understood is that it brings about pressure changes that disturbs velocity field and thus in turn disturbs continuity back. This cycle does not allow residuals to go down as some sort of convergence divergence going on. By multiplying this grad term by some factor like 0.1 or 0.2 , I could see residuals smoothly going down. I have personally decided to now drop coupled solver from my code (it is there but user cant switch it on) and decided to create another algo. My reasons were cost of solving coupled system was high (higher than 2 iterations of simple) and convergence is not dramatic in most of what I tested. In future, I might visit coupled solver but for now I leave it. |
||
|
|

|
||
|
|
|
#20 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Also coupled solver does not always mean many times faster convergence. Here for example for this test case, my solver's SIMPLE can out run pressure based coupled solver of Fluent. (The extend algorithm actually could do this test case in 350 iterations).
PS: For comparison, starccm SIMPLE drop residuals to 1E-12 in 600 iterations and then residuals stall. Since CCM is another commercial code, its worth knowing. I dropped coupled solver in favour of simple-extend algo since 1 iteration of extend takes 1.5 iterations of SIMPLE and I expect to drop the cost further to 1.2 or so of SIMPLE iteration. In this situation I expect it to out perform coupled most of the time. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [ANSYS Meshing] Help with element size | sandri_92 | ANSYS Meshing & Geometry | 14 | November 14, 2018 07:54 |
| Pressure equation for compressible solver | Akshay | OpenFOAM Programming & Development | 8 | October 3, 2015 09:22 |
| Pressure Based Solver, Transient flow | mnolan93 | FLUENT | 0 | May 16, 2015 09:37 |
| Star cd es-ice solver error | ernarasimman | STAR-CD | 2 | September 12, 2014 00:01 |
| Pressure based vs density based solver | newbie384 | FLUENT | 2 | July 5, 2013 02:04 |