 |
|
|
[Sponsors] | |||||
Configuration of BCs for linear acoustic simulation using FV Godunov's scheme |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Adrian
Join Date: Oct 2016
Posts: 12
Rep Power: 9  |
Dear all,
I have implemented a 2D finite volume Godunov scheme for the computation of the linear acoustics problem (linearized isentropic Euler eqs.) using structured quadrilateral grid in the cartesian coordinate system. More details on the problem and the numerical method used can be found in LeVeque, R. J. (2002). Finite volume methods for hyperbolic problems (Vol. 31). Cambridge university press., section 21.4 Acoustics. Now, I am trying to implement the boundary conditions. Up to this point, I compute the numerical fluxes at the boundaries by means of the Riemann invariants w1, w2 and w3. For the outgoing BC, w1 is the incoming invariant to the wall from outside of the domain and w3 is the incoming invariant from the last cell of the domain. The invariants read 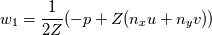 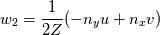 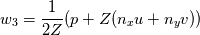 To consider whether reflection or absorption must take place, I have defined a reflection coefficient as 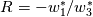 Notice that superscript * denotes the evaluation at the interface while subscript i denotes the evaluation at the cell touching the interface. For instance, when seeking non-reflecting BC, R=0, hence w1=0, which means that no information arrives to the interface from outside of the domain. The value of the variables at the interface will be computed ensuring the conservation of the w3 invariant from the center of the last cell to the wall, taking into account that w1=0 in this particular case. Hence we have 2 unknowns and 2 equations 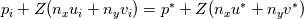 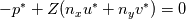 In the more general case where R is still undefined, the three components of the numerical flux at interfaces normal to the x-direction are computed as: 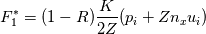 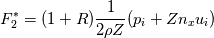 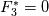 where 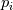 and and 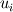 are the pressure and velocity on the cell touching the interface, and are the pressure and velocity on the cell touching the interface, and  the x component of the normal vector of the cell edge, which in this case will be 1 or -1. the x component of the normal vector of the cell edge, which in this case will be 1 or -1.This technique is similar to that presented by Leveque in the aforementioned book using ghost cells, at least in 1D. If setting R=0 and computing perturbations only in one space dimension, say the y-component of the velocity is zero in the whole domain, I obtain the sought results, however, when waves move in oblique directions with respect to the cartesian directions, some part of the waves are reflected. I cannot understand the reason for such behavior, since I use quadrilateral grid and the component of the velocity paralell to the interface should not influence the solution and the problem should be equivalent to a 1D case. Can anybody help me to understand this issue? Thanks and best regards,
__________________
Adrián |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Could you post the figures?
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Adrian
Join Date: Oct 2016
Posts: 12
Rep Power: 9  |
Please find attached to this post the results for the pressure when computing the evolution of a initial pressure gaussian profile. Results are shown at three different times. It can be observed in the right plot that two refected waves moving to the center appear.
As mentioned before, if the wave front was a perfectly vertical wave, that is, only with velocity in the x-component, it would not generate any reflection. Thanks again.
__________________
Adrián |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
have you checked your BC.s for the pure 1D problem? does it reproduce the same effect?
How did you define the invariant for 2d problems? |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Adrian
Join Date: Oct 2016
Posts: 12
Rep Power: 9  |
Thanks for your reply. Yes, I have computed different test cases considering symmetry in the y-axis and velocity in y equal to zero, which is equivalent to a pure 1D problem in X and the BCs behave as expected: when setting R=0 the whole wave is transmited and when setting R=1 the whole wave is reflected.
For the 2D case, I have derived the Riemann invariants from the normal Riemann problem, which is the RP projected onto the normal surface vector. In this way, I obtain 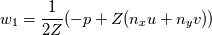 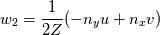 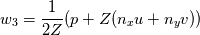 associated to the 1, 2 and 3-characteristic fields. Such fields are linear with constant wave speed 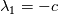 , , 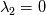 and and 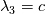 . .Then, I apply the conservation of the third invariant as 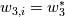 , that is, the value of the invariant inside the cell is equal to the value of the invariant at the interface. Moreover, I use the relation , that is, the value of the invariant inside the cell is equal to the value of the invariant at the interface. Moreover, I use the relation 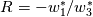 , and finally obtain the numerical fluxes outlined in the first post by solving the two previous equations for p* and u*, or p* and v*, and multiplying by the coefficient matrix of the normal RP that relates flux and states. I don't know what I am missing... Is there any other way of doing this? , and finally obtain the numerical fluxes outlined in the first post by solving the two previous equations for p* and u*, or p* and v*, and multiplying by the coefficient matrix of the normal RP that relates flux and states. I don't know what I am missing... Is there any other way of doing this?
__________________
Adrián |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I am not sure about that, I worked time ago and I can be wrong ...in a 2D problem you cannot define the invariant functions satisfying the full diagonalized system, right?
So you have an approximation for "invariant" function. You can work by dimensional factorization but however the initial multidimensional system is approximated. Maybe what you see is a second order effect of that. |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Adrian
Join Date: Oct 2016
Posts: 12
Rep Power: 9  |
Thank you for your help Filippo!! That is true, the Riemann invariants will only satisfy the 1D split of the system, or as you have said, they cannot satisfy the full diagonalized system..
I was afraid it had to do with something related to this issue... Do you know any useful reference on this topic to properly implement the BC?
__________________
Adrián |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
You can search by google, there are a lot of studies
 you can start also from the Leveque book, sec.21.8 and the cited references. |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Adrian
Join Date: Oct 2016
Posts: 12
Rep Power: 9  |
Thanks for your help!
Best regards!
__________________
Adrián |
|
|
|

|
|
 |
| Tags |
| acoustics, boundary conditons, finite volume method, non-reflecting, riemann invariant |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| BCs in an FSI simulation of a flexble pipe | vivekcfd | OpenFOAM | 10 | January 8, 2010 04:14 |
| acoustic and noise simulation | Daniel Moussavi | Siemens | 2 | August 10, 2009 05:01 |
| Best Pc Configuration for maximum simulation speed | Anastasios Georgoulas | FLUENT | 2 | December 18, 2008 12:34 |
| Acoustic simulation | Hugh | FLUENT | 0 | October 1, 2006 21:54 |
| Difficult BCs about Freesurface Simulation by VOF | Yongguang Cheng | FLUENT | 0 | September 19, 2003 07:39 |