 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Mar 2017
Posts: 7
Rep Power: 9  |
I'm trying to implement a simple minmod limiter on my primitive variables.
It (seemingly) works perfectly when advecting a square pulse (u=p=const) but is worse than piecewise constant at Sod's problem (see pics). Here is how I'm calculating the edge states: Code:
leftDiff = rho[i-1] - rho[i-2]; rightDiff = rho[i] - rho[i-1]; left.rho = rho[i-1] + 0.5 * minmod(leftDiff, rightDiff); //... leftDiff = rho[i] - rho[i-1]; rightDiff = rho[i+1] - rho[i]; right.rho = rho[i] + 0.5 * minmod(leftDiff, rightDiff); //... |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I guess it depends on what you are doing in your "minmod" function. I am used to seeing fluxes interpolated based on:
phi_f = phi_0 + 0.5*psi(r)*(phi_0 - phi_-1) where r = (phi_1 - phi_0)/(phi_0 - phi_-1) and for minmod, psi(r) = max(0,min(1,r)) (This all assumes evenly spaced grids. Also, I am used to using slope limiters on unstructured meshes, so my flux-limiter Fu is a little rusty.) if your minmod performs those same calculations and returns a dimensional value for density, then it should be right. But r in the forms I am used to seeing is dimensionless, as is the return value of minmod(). So, I'd expect a trailing factor of units of density to make it physical in your right.rho and left.rho lines. |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Join Date: Mar 2017
Posts: 7
Rep Power: 9  |
Quote:
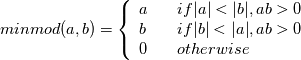
|
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
I think your problem does not come only from 2nd order reconstruction. Your 1st order solution does not look TVD to me, large oscillations near the shock do not occur when using shock capturing upwind fluxes. What spatial discretisation are you using ?
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I agree, Godunov must give a monotonic solution
|
|
|
|

|
|
|
|
|
#6 |
|
New Member
Join Date: Mar 2017
Posts: 7
Rep Power: 9  |
I'm using finite volume. What kind of things can I do to find the problem?
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
What Riemann solver are you using ? If it is the exact or Roe flux, maybe you should start with the simplest one: the Rusanov flux. As it seems that the raréfaction and contact are Well captured it may be à bug with the définition of left and right pressure as they are discontinuous across the shock
|
|
|
|

|
|
|
|
|
#8 | |
|
New Member
Join Date: Mar 2017
Posts: 7
Rep Power: 9  |
Quote:
|
||
|
|

|
||
|
|
|
#9 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Hello,
I haven't looked much the code you are referring to. I can't recommend you taking pieces of code as a black box, the mistake could be in that code, the way you use it or both. It is worth taking time to learn how the exact solution is built (Toro, Riemann Solvers and Numerical Methods for Fluid Dynamics is one of the references) and how approximate solvers have been derived. This way you will understand the code you mention and find what is wrong. Cheers, François |
|
|
|

|
|
 |
| Tags |
| euler, limiter, minmod, plm, sod |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Minmod limiter for Correction Procedure via Reconstruction | LUQILIN | Main CFD Forum | 0 | May 20, 2016 02:36 |
| Is MINMOD still an option for slope limiter? | wruudf | SU2 | 5 | October 22, 2014 18:13 |
| Limiter MINMOD' problems | akun646 | SU2 | 3 | August 28, 2014 15:24 |
| how to implement MINMOD limiter ? | alan | Main CFD Forum | 0 | November 25, 2008 10:57 |
| Moment limiter in DG method. | jinwon park | Main CFD Forum | 0 | May 15, 2008 12:18 |