 |
|
|
[Sponsors] | |||||
Periodic boundary conditions for compressible Euler equations |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi,
I am currently building up a 2D hydrodynamics code. Specifically, I am numerically solving the 2D Euler equations in order to simulate Kelvin-Helmholtz instability. The boundary conditions are periodic, however I am running into issues when enforcing such conditions. Given the governing equations 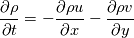 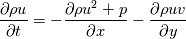 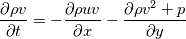 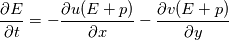 I define Q to be the left-hand side of the system of PDEs. As such in discrete form its a (nx,ny,4) array. Given we have periodic boundary conditions I set Q(1,1:ny,1:4) = Q(nx,1:ny,1:4) (Q(1) = Q(n) in x) Q(1:nx,1,1:4) = Q(1:nx,ny,1:4) (Q(1) = Q(n) in y) With this implementation I am not getting the desired effects of the Kelvin-Helmholtz. I conclude the error is at the boundary due to the plot. I start my arrays at 1 so my boundaries are at 1 and nx. Code:
subroutine BC (Q_out)
implicit none
real, dimension(nx,ny,4), intent(inout) :: Q_out
Q_out(1,:,:) = Q_out(nx,:,:)
Q_out(:,1,:) = Q_out(:,ny,:)
return
end subroutine
NOTE 1: I can post my Fortran code if it will help. NOTE 2: I have tested this code on various 2D Riemann problems and I get correct results. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
"I define Q to be the left-hand side of the system of PDEs."
 Maybe the RHS? Have you tried to set periodicity on the fluxes? |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi Denaro,
Sorry for not being more precise. I meant to say that Q is the left-hand side (time-derivative terms) of the hyperbolic system. In terms of applying the boundary conditions to the fluxes, I have tried that with little luck. Code:
function RHS (Q_in, p, c)
implicit none
real, dimension(nx,ny), intent(in) :: p, c
real, dimension(nx,ny) :: r, u, v, E
real, dimension(nx,ny,4) :: F, G, RHS, Q_in
real, dimension(nx-1,ny) :: axh
real, dimension(nx,ny-1) :: ayh
real, dimension(nx-1,ny,4) :: Fh
real, dimension(nx,ny-1,4) :: Gh
integer :: i, j, k
do k=1,4
do j=1,ny
do i=1,nx
r(i,j) = Q_in(i,j,1)
u(i,j) = Q_in(i,j,2)/r(i,j)
v(i,j) = Q_in(i,j,3)/r(i,j)
E(i,j) = Q_in(i,j,4)
F(i,j,1) = r(i,j)*u(i,j)
F(i,j,2) = r(i,j)*u(i,j)**2.0 + p(i,j)
F(i,j,3) = r(i,j)*u(i,j)*v(i,j)
F(i,j,4) = u(i,j)*(E(i,j) + p(i,j))
G(i,j,1) = r(i,j)*v(i,j)
G(i,j,2) = r(i,j)*u(i,j)*v(i,j)
G(i,j,3) = r(i,j)*v(i,j)**2.0 + p(i,j)
G(i,j,4) = v(i,j)*(E(i,j) + p(i,j))
end do
end do
do j=1,ny-1
do i=1,nx-1
axh(i,j) = max(abs(u(i,j)) + c(i,j), abs(u(i+1,j)) + c(i+1,j))
Fh(i,j,k) = 0.5*(F(i,j,k) + F(i+1,j,k) - axh(i,j)*(Q(i+1,j,k) - Q(i,j,k)))
end do
end do
do j=1,ny-1
do i=1,nx-1
ayh(i,j) = max(abs(v(i,j)) + c(i,j), abs(v(i,j+1)) + c(i,j+1))
Gh(i,j,k) = 0.5*(G(i,j,k) + G(i,j+1,k) - ayh(i,j)*(Q(i,j+1,k) - Q(i,j,k)))
end do
end do
do j=2,ny-1
do i=2,nx-1
RHS(i,j,k) = - (Fh(i,j,k) - Fh(i-1,j,k))/dx - (Gh(i,j,k) - Gh(i,j-1,k))/dy
end do
end do
CALL BC(RHS)
end do
return
end function RHS
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
As I wrote, you have to set the same fluxes
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Jul 2009
Posts: 357
Rep Power: 19  |
If you are resetting the boundary values after the flux evaluation, then as FMDenaro points out, your flux values won't match the Q values. So you can either reset the flux values or call your BC routine prior to the flux evaluation.
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi Guys,
Thanks for the comments. I will try it out when I get to a computer. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi,
So if I'm understanding what you said, I tried called my BC subroutine before the flux evaluations: Code:
function RHS (Q_in, p, c)
implicit none
real, dimension(nx,ny), intent(in) :: p, c
real, dimension(nx,ny) :: r, u, v, E
real, dimension(nx,ny,4) :: F, G, RHS, Q_in
real, dimension(nx-1,ny) :: axh
real, dimension(nx,ny-1) :: ayh
real, dimension(nx-1,ny,4) :: Fh
real, dimension(nx,ny-1,4) :: Gh
integer :: i, j, k
do k=1,4
do j=1,ny
do i=1,nx
r(i,j) = Q_in(i,j,1)
u(i,j) = Q_in(i,j,2)/r(i,j)
v(i,j) = Q_in(i,j,3)/r(i,j)
E(i,j) = Q_in(i,j,4)
F(i,j,1) = r(i,j)*u(i,j)
F(i,j,2) = r(i,j)*u(i,j)**2.0 + p(i,j)
F(i,j,3) = r(i,j)*u(i,j)*v(i,j)
F(i,j,4) = u(i,j)*(E(i,j) + p(i,j))
G(i,j,1) = r(i,j)*v(i,j)
G(i,j,2) = r(i,j)*u(i,j)*v(i,j)
G(i,j,3) = r(i,j)*v(i,j)**2.0 + p(i,j)
G(i,j,4) = v(i,j)*(E(i,j) + p(i,j))
end do
end do
CALL BC(RHS)
do j=1,ny
do i=1,nx-1
axh(i,j) = max(abs(u(i,j)) + c(i,j), abs(u(i+1,j)) + c(i+1,j))
Fh(i,j,k) = 0.5*(F(i,j,k) + F(i+1,j,k) - axh(i,j)*(Q(i+1,j,k) - Q(i,j,k)))
end do
end do
do j=1,ny-1
do i=1,nx
ayh(i,j) = max(abs(v(i,j)) + c(i,j), abs(v(i,j+1)) + c(i,j+1))
Gh(i,j,k) = 0.5*(G(i,j,k) + G(i,j+1,k) - ayh(i,j)*(Q(i,j+1,k) - Q(i,j,k)))
end do
end do
do j=2,ny-1
do i=2,nx-1
RHS(i,j,k) = - (Fh(i,j,k) - Fh(i-1,j,k))/dx - (Gh(i,j,k) - Gh(i,j-1,k))/dy
end do
end do
end do
return
end function RHS
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Immagine a flux vector fluxes_species(1:N) and the periodicity being between 1 and N and where fluxes_species(i) is at the left side of the components species(i). So the update of the species(1) depends on the difference
fluxes_species(2)-fluxes_species(1) where fluxes_species(1) lies on the left boundary and must be computed. When you arrive to compute the update of species(N) you should compute the difference fluxes_species(N+1)-fluxes_species(N) that setting the periodicity becomes fluxes_species(1)-fluxes_species(N) |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Jul 2009
Posts: 357
Rep Power: 19  |
You want the Q values to match, prior to the evaluation of the fluxes F and G.
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
I do not understand the vector you pass to the subroutine BC. You send RHS which is the sum of the fluxes for each element, it is equivalent to say dQ1/dt = dQn/dt, the update of conservative variables in the first and last cell are equal, which is not true in general.
As FMDenaro suggested, you have to enforce periodicity on the fluxes of the boundary of the domain, not on the sum of fluxes of bounding elements (RHS). What goes out on one side enters the other side. If you use ghost cells you can very easily enforce periodicity on the conservative variables before evaluating the fluxes the normal way. Q_in(0,:,  =Q_in(nx,:, =Q_in(nx,:, (ghost cell left = last layer of real cells), the same for cell layers i=nx+1, j=0, j=ny+1. (ghost cell left = last layer of real cells), the same for cell layers i=nx+1, j=0, j=ny+1. Have a look to the book of Blazek (COMPUTATIONAL FLUID DYNAMICS: PRINCIPLES AND APPLICATIONS), section 8.7 periodic boundary conditions |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi all,
Thank you for the helpful replies. I have opted to try and implement the periodic boundary conditions via ghost points. With that said I have some question: 1. When using ghost points in this context my arrays are (nx,ny) for Q, (nx-1,ny,4) for F_half, and (nx,ny-1,4) for G_half. Does that mean My arrays for Q have to be (-1:nx+1,-1:ny+1,4)? the -1 in the array is to account for the -1 ghost point. In terms of calling my periodic BC routine prior to the total flux evaluation (RHS), I have tried doing the following Fh(1,:,: ) = Fh(nx-1,:,: ) Fh(:,1,: ) = Fh(:,ny,: ) Gh(1,:,: ) = Gh(nx,:,: ) Gh(:,1,: ) = Gh(:,ny-1,: ) I choose nx-1 and ny-1 for Fh and Gh respectively as they are sizes (nx-1,ny,4) and (nx,ny-1,4). Yet, I still do not get the correct results. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
If you are using colocated grid, the things are the same in x and y direction. If the periodicity in one general direction is between node 1 and node N then you have for a general function the links
f(0)=f(N-1) f(-1)=f(N-2) .... and f(N+1)=f(2) f(N+2)=f(3) .... |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi Dr. Denaro,
That clears up a lot of questions. I'm working on a uniform grid currently. So given I have a first order accurate discretization (in space) I have points Code:
i=i-1, i, i+1 j=j-1, j, j+1 Code:
u(0) = u(nx-1) u(1) = u(nx) u(2) = u(nx+1) Code:
real, dimension(-1:nx+1,-1:ny+1) :: Q |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi everyone,
After some odd days I am still sheepishly coming back with no luck. I feel like I have tried almost everything. Attached is my main time loop and my RHS with my most recent attempt. The two code snippets are where I am enforcing boundary conditions. For purposes of clarity I am using the Shu TVD Runge-Kutta 3. Main time loop for advancing the solutions Code:
t = 0.D0
do while (t < tEnd)
do j=1,ny
do i=1,nx
Q(i,j,1) = r(i,j)
Q(i,j,2) = r(i,j)*u(i,j)
Q(i,j,3) = r(i,j)*v(i,j)
Q(i,j,4) = E(i,j)
end do
end do
Q1 = Q + dt*RHS(Q, c, p, H)
Q1(1,:,:) = Q1(nx,:,:)
Q1(:,1,:) = Q1(:,ny,:)
Q2 = (3D+0/4D+0)*Q + (1D+0/4D+0)*Q1 + (1D+0/4D+0)*dt*RHS(Q1, c, p, H)
Q2(1,:,:) = Q2(nx,:,:)
Q2(:,1,:) = Q2(:,ny,:)
Qn = (1D+0/3D+0)*Q + (2D+0/3D+0)*Q2 + (2D+0/3D+0)*dt*RHS(Q2, c, p, H)
Qn(:,1,:) = Qn(:,ny,:)
Qn(1,:,:) = Qn(ny,:,:)
Q = Qn
r = Qn(:,:,1)
u = Qn(:,:,2)/Qn(:,:,1)
v = Qn(:,:,3)/Qn(:,:,1)
E = Qn(:,:,4)
p = (gamma-1)*(E - (0.5D+00*r)*(u**2.D0 + v**2.D0))
c = sqrt(gamma*p/r)
H = 0.5D+00*(u**2 + v**2) + c**2/(gamma-1)
t = t + dt
print *,'t=',t
end do
Code:
function RHS (Q_in, c, p, H) implicit none real, dimension(nx,ny,4), intent(inout) :: Q_in real, dimension(nx,ny), intent(in) :: c, p, H real, dimension(nx,ny) :: Mxm, Mxp, Mym, Myp real, dimension(nx,ny) :: pxp, pxm, pyp, pym real, dimension(nx-1,ny) :: pxh real, dimension(nx,ny-1) :: pyh real, dimension(nx,ny-1) :: My1, My2, Myh real, dimension(nx-1,ny) :: Mx1, Mx2, Mxh real, dimension(nx,ny) :: Mxch, Mych real, dimension(nx,ny,4) :: Fh real, dimension(nx,ny,4) :: Gh real, dimension(nx-1,ny) :: cxh real, dimension(nx,ny-1) :: cyh real, dimension(nx,ny,4) :: RHS real, dimension(nx,ny) :: r, u, v, E integer :: i, j, k do j=1,ny do i=1,nx r(i,j) = Q_in(i,j,1) u(i,j) = Q_in(i,j,2)/Q_in(i,j,1) v(i,j) = Q_in(i,j,3)/Q_in(i,j,1) E(i,j) = Q_in(i,j,4) end do end do do j=1,ny do i=1,nx-1 cxh(i,j) = sqrt(c(i,j)*c(i+1,j)) Mxch(i,j) = u(i,j)/cxh(i,j) end do end do do j=1,ny do i=1,nx if (abs(Mxch(i,j)) >= 1) then Mxp(i,j) = 0.5D+00*(Mxch(i,j) + abs(Mxch(i,j))) Mxm(i,j) = 0.5D+00*(Mxch(i,j) - abs(Mxch(i,j))) pxp(i,j) = 0.5D+00*(1.0D+00 + sign(onez,Mxch(i,j))) pxm(i,j) = 0.5D+00*(1.0D+00 - sign(onez,Mxch(i,j))) else Mxp(i,j) = 0.25*(Mxch(i,j) + 1)**2 + beta*(Mxch(i,j)**2 - 1)**2 Mxm(i,j) = -0.25*(Mxch(i,j) - 1)**2 - beta*(Mxch(i,j)**2 - 1)**2 pxp(i,j) = 0.25*(Mxch(i,j) + 1)**2*(2 - Mxch(i,j)) + alpha*Mxch(i,j)*(Mxch(i,j)**2 - 1)**2 pxm(i,j) = 0.25*(Mxch(i,j) - 1)**2*(2 + Mxch(i,j)) - alpha*Mxch(i,j)*(Mxch(i,j)**2 - 1)**2 end if end do end do do j=1,ny do i=1,nx-1 Mxh(i,j) = Mxp(i,j) + Mxm(i+1,j) Mx1(i,j) = 0.5D+00*(Mxh(i,j) + abs(Mxh(i,j))) Mx2(i,j) = 0.5D+00*(Mxh(i,j) - abs(Mxh(i,j))) pxh(i,j) = pxp(i,j)*p(i,j) + pxm(i+1,j)*p(i+1,j) end do end do do j=1,ny-1 do i=1,nx cyh(i,j) = sqrt(c(i,j)*c(i,j+1)) Mych(i,j) = v(i,j)/cyh(i,j) end do end do do j=1,ny do i=1,nx if (abs(Mych(i,j)) >= 1) then Myp(i,j) = 0.5D+00*(Mych(i,j) + abs(Mych(i,j))) Mym(i,j) = 0.5D+00*(Mych(i,j) - abs(Mych(i,j))) pyp(i,j) = 0.5D+00*(1.0D+00 + sign(onez,Mych(i,j))) pym(i,j) = 0.5D+00*(1.0D+00 - sign(onez,Mych(i,j))) else Myp(i,j) = 0.25D+00*(Mych(i,j) + 1)**2 + beta*(Mych(i,j)**2 - 1)**2 Mym(i,j) = -0.25D+00*(Mych(i,j) - 1)**2 - beta*(Mych(i,j)**2 - 1)**2 pyp(i,j) = 0.25D+00*(Mych(i,j) + 1)**2*(2 - Mych(i,j)) + alpha*Mych(i,j)*(Mych(i,j)**2 - 1)**2 pym(i,j) = 0.25D+00*(Mych(i,j) - 1)**2*(2 + Mych(i,j)) - alpha*Mych(i,j)*(Mych(i,j)**2 - 1)**2 end if end do end do do j=1,ny-1 do i=1,nx Myh(i,j) = Myp(i,j) + Mym(i,j+1) My1(i,j) = 0.5D+00*(Myh(i,j) + abs(Myh(i,j))) My2(i,j) = 0.5D+00*(Myh(i,j) - abs(Myh(i,j))) pyh(i,j) = pyp(i,j)*p(i,j) + pym(i,j+1)*p(i,j+1) end do end do Fh(1,:,:) = Fh(nx-1,:,:) Fh(:,1,:) = Fh(:,ny,:) do j=1,ny do i=1,nx-1 Fh(i,j,1) = cxh(i,j)*(Mx1(i,j)*r(i,j) + Mx2(i,j)*r(i+1,j)) Fh(i,j,2) = cxh(i,j)*(Mx1(i,j)*r(i,j)*u(i,j) + Mx2(i,j)*r(i+1,j)*u(i+1,j)) + pxh(i,j) Fh(i,j,3) = cxh(i,j)*(Mx1(i,j)*r(i,j)*v(i,j) + Mx2(i,j)*r(i+1,j)*v(i+1,j)) Fh(i,j,4) = cxh(i,j)*(Mx1(i,j)*r(i,j)*H(i,j) + Mx2(i,j)*r(i+1,j)*H(i+1,j)) end do end do Gh(1,:,:) = Gh(nx,:,:) Gh(:,1,:) = Gh(:,ny-1,:) do j=1,ny-1 do i=1,nx Gh(i,j,1) = cyh(i,j)*(My1(i,j)*r(i,j) + My2(i,j)*r(i,j+1)) Gh(i,j,2) = cyh(i,j)*(My1(i,j)*r(i,j)*u(i,j) + My2(i,j)*r(i,j+1)*u(i,j+1)) Gh(i,j,3) = cyh(i,j)*(My1(i,j)*r(i,j)*v(i,j) + My2(i,j)*r(i,j+1)*v(i,j+1)) + pyh(i,j) Gh(i,j,4) = cyh(i,j)*(My1(i,j)*r(i,j)*H(i,j) + My2(i,j)*r(i,j+1)*H(i,j+1)) end do end do do k=1,4 do j=2,ny-1 do i=2,nx-1 RHS(i,j,k) = - (Fh(i,j,k) - Fh(i-1,j,k))/dx - (Gh(i,j,k) - Gh(i,j-1,k))/dy end do end do end do end function RHS |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Sorry to say that I think you have not programmed correctly the BC.s.
I give you a very simple 1D example. Consider the domain going from node 1 (x=0) to node N (x=L). Therefore, the periodicity is such that any function f has f(1)=f(N). As a consequence, in terms of ghost nodes you have f(0)=f(N-1) and f(N+1)=f(2). Let us work with a first order FD discretization of the linear wave equation (u>0): fold will be prescribed for i=1,N fnew(1)=fold(1) -u*dt*(fold(1)-fold(N-1))/dx do i=2,N-1 fnew(i)=fold(i) -u*dt*(fold(i)-fold(i-1))/dx end do fnew(N)=fnew(1) then swap the vector fnew to fold and continue the cycle in t. A finite volume discretization is slightly different. You have to work on the flux function to be computed on each face and inserted in the equation fav_new(i)=fav_old(i) -dt*(flux(i+1/2)-flux(i-1/2))/dx so that you prescribe the periodicity on the vector flux |
|
|
|

|
|
|
|
|
#16 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi FM Denaro,
Thank you for your patience on this thread. I will digest this and try to implement this in my solver. EDIT: So what I'm doing wrong is that I need to be evaluating the flux "manually" i.e. what you did for fnew outside the interior loop? |
|
|
|

|
|
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
If you do not want to treat explicitly the equation wher the BC enters into, then you have to use ghost points. Therefore, you start at t0 prescribing fold for i=0:N+1 then compute fnew(1) using the general scheme in the interior. Do not forget to explicitly set the BC for fnew(0), fnew(N+1). |
||
|
|

|
||
|
|
|
#18 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi again,
I have implemented your suggestion on ghost points, but again I am getting incorrect results. To be sure I have posted my code. Code:
real, dimension(nx,ny) :: x, y
real, dimension(0:nx+1,0:ny+1) :: r0, u0, v0, p0, E0, H0
real, dimension(0:nx+1,0:ny+1) :: r, u, v, p, E, H, c0, c
real, dimension(0:nx+1,0:ny+1,4) :: Q, Q1, Q2, Qn
real, dimension(nx,ny,2) :: Eigenvalue
t = 0.D0
do while (t < tEnd)
do j=0,ny+1
do i=0,nx+1
Q(i,j,1) = r(i,j)
Q(i,j,2) = r(i,j)*u(i,j)
Q(i,j,3) = r(i,j)*v(i,j)
Q(i,j,4) = E(i,j)
end do
end do
Q1(0,:,:) = Q1(nx-1,:,:)
Q1(:,0,:) = Q1(:,ny-1,:)
Q1(1,:,:) = Q1(nx,:,:)
Q1(:,1,:) = Q1(:,ny,:)
Q1(2,:,:) = Q1(nx+1,:,:)
Q1(:,2,:) = Q1(:,ny+1,:)
Q1 = Q + dt*RHS(Q, c, p, H)
Q2(0,:,:) = Q2(nx-1,:,:)
Q2(:,0,:) = Q2(:,ny-1,:)
Q2(1,:,:) = Q2(nx,:,:)
Q2(:,1,:) = Q2(:,ny,:)
Q2(2,:,:) = Q2(nx+1,:,:)
Q2(:,2,:) = Q2(:,ny+1,:)
Q2 = (3D+0/4D+0)*Q + (1D+0/4D+0)*Q1 + (1D+0/4D+0)*dt*RHS(Q1, c, p, H)
Qn(0,:,:) = Qn(nx-1,:,:)
Qn(:,0,:) = Qn(:,ny-1,:)
Qn(:,1,:) = Qn(:,nx,:)
Qn(1,:,:) = Qn(ny,:,:)
Qn(2,:,:) = Qn(nx+1,:,:)
Qn(:,2,:) = Qn(:,ny+1,:)
Qn = (1D+0/3D+0)*Q + (2D+0/3D+0)*Q2 + (2D+0/3D+0)*dt*RHS(Q2, c, p, H)
Q1 = Qn
Q2 = Qn
Q = Qn
r = Qn(:,:,1)
u = Qn(:,:,2)/Qn(:,:,1)
v = Qn(:,:,3)/Qn(:,:,1)
E = Qn(:,:,4)
p = (gamma-1)*(E - (0.5D+00*r)*(u**2.D0 + v**2.D0))
c = sqrt(gamma*p/r)
H = 0.5D+00*(u**2 + v**2) + c**2/(gamma-1)
t = t + dt
print *,'t=',t
end do
Code:
function RHS (Q_in, c, p, H) implicit none real, dimension(0:nx+1,0:ny+1,4), intent(inout) :: Q_in real, dimension(0:nx+1,0:ny+1), intent(in) :: c, p, H real, dimension(nx,ny) :: Mxm, Mxp, Mym, Myp real, dimension(nx,ny) :: pxp, pxm, pyp, pym real, dimension(nx-1,ny) :: pxh real, dimension(nx,ny-1) :: pyh real, dimension(nx,ny-1) :: My1, My2, Myh real, dimension(nx-1,ny) :: Mx1, Mx2, Mxh real, dimension(nx,ny) :: Mxch, Mych real, dimension(0:nx+1,0:ny+1,4) :: Fh real, dimension(0:nx+1,0:ny+1,4) :: Gh real, dimension(nx-1,ny) :: cxh real, dimension(nx,ny-1) :: cyh real, dimension(0:nx+1,0:ny+1,4) :: RHS real, dimension(0:nx+1,0:ny+1) :: r, u, v, E integer :: i, j, k do j=1,ny do i=1,nx r(i,j) = Q_in(i,j,1) u(i,j) = Q_in(i,j,2)/Q_in(i,j,1) v(i,j) = Q_in(i,j,3)/Q_in(i,j,1) E(i,j) = Q_in(i,j,4) end do end do do j=1,ny do i=1,nx-1 cxh(i,j) = sqrt(c(i,j)*c(i+1,j)) Mxch(i,j) = u(i,j)/cxh(i,j) end do end do do j=1,ny do i=1,nx if (abs(Mxch(i,j)) >= 1) then Mxp(i,j) = 0.5D+00*(Mxch(i,j) + abs(Mxch(i,j))) Mxm(i,j) = 0.5D+00*(Mxch(i,j) - abs(Mxch(i,j))) pxp(i,j) = 0.5D+00*(1.0D+00 + sign(onez,Mxch(i,j))) pxm(i,j) = 0.5D+00*(1.0D+00 - sign(onez,Mxch(i,j))) else Mxp(i,j) = 0.25*(Mxch(i,j) + 1)**2 + beta*(Mxch(i,j)**2 - 1)**2 Mxm(i,j) = -0.25*(Mxch(i,j) - 1)**2 - beta*(Mxch(i,j)**2 - 1)**2 pxp(i,j) = 0.25*(Mxch(i,j) + 1)**2*(2 - Mxch(i,j)) + alpha*Mxch(i,j)*(Mxch(i,j)**2 - 1)**2 pxm(i,j) = 0.25*(Mxch(i,j) - 1)**2*(2 + Mxch(i,j)) - alpha*Mxch(i,j)*(Mxch(i,j)**2 - 1)**2 end if end do end do do j=1,ny do i=1,nx-1 Mxh(i,j) = Mxp(i,j) + Mxm(i+1,j) Mx1(i,j) = 0.5D+00*(Mxh(i,j) + abs(Mxh(i,j))) Mx2(i,j) = 0.5D+00*(Mxh(i,j) - abs(Mxh(i,j))) pxh(i,j) = pxp(i,j)*p(i,j) + pxm(i+1,j)*p(i+1,j) end do end do do j=1,ny-1 do i=1,nx cyh(i,j) = sqrt(c(i,j)*c(i,j+1)) Mych(i,j) = v(i,j)/cyh(i,j) end do end do do j=1,ny do i=1,nx if (abs(Mych(i,j)) >= 1) then Myp(i,j) = 0.5D+00*(Mych(i,j) + abs(Mych(i,j))) Mym(i,j) = 0.5D+00*(Mych(i,j) - abs(Mych(i,j))) pyp(i,j) = 0.5D+00*(1.0D+00 + sign(onez,Mych(i,j))) pym(i,j) = 0.5D+00*(1.0D+00 - sign(onez,Mych(i,j))) else Myp(i,j) = 0.25D+00*(Mych(i,j) + 1)**2 + beta*(Mych(i,j)**2 - 1)**2 Mym(i,j) = -0.25D+00*(Mych(i,j) - 1)**2 - beta*(Mych(i,j)**2 - 1)**2 pyp(i,j) = 0.25D+00*(Mych(i,j) + 1)**2*(2 - Mych(i,j)) + alpha*Mych(i,j)*(Mych(i,j)**2 - 1)**2 pym(i,j) = 0.25D+00*(Mych(i,j) - 1)**2*(2 + Mych(i,j)) - alpha*Mych(i,j)*(Mych(i,j)**2 - 1)**2 end if end do end do do j=1,ny-1 do i=1,nx Myh(i,j) = Myp(i,j) + Mym(i,j+1) My1(i,j) = 0.5D+00*(Myh(i,j) + abs(Myh(i,j))) My2(i,j) = 0.5D+00*(Myh(i,j) - abs(Myh(i,j))) pyh(i,j) = pyp(i,j)*p(i,j) + pym(i,j+1)*p(i,j+1) end do end do Fh(0,:,:) = Fh(nx-1,:,:) Fh(:,0,:) = Fh(:,ny,:) Fh(1,:,:) = Fh(nx,:,:) Fh(:,1,:) = Fh(:,ny,:) Fh(2,:,:) = Fh(nx+1,:,:) Fh(:,2,:) = Fh(:,ny+1,:) do j=1,ny do i=1,nx-1 Fh(i,j,1) = cxh(i,j)*(Mx1(i,j)*r(i,j) + Mx2(i,j)*r(i+1,j)) Fh(i,j,2) = cxh(i,j)*(Mx1(i,j)*r(i,j)*u(i,j) + Mx2(i,j)*r(i+1,j)*u(i+1,j)) + pxh(i,j) Fh(i,j,3) = cxh(i,j)*(Mx1(i,j)*r(i,j)*v(i,j) + Mx2(i,j)*r(i+1,j)*v(i+1,j)) Fh(i,j,4) = cxh(i,j)*(Mx1(i,j)*r(i,j)*H(i,j) + Mx2(i,j)*r(i+1,j)*H(i+1,j)) end do end do Gh(0,:,:) = Gh(nx-1,:,:) Gh(:,0,:) = Gh(:,ny,:) Gh(1,:,:) = Gh(nx,:,:) Gh(:,1,:) = Fh(:,ny,:) Gh(2,:,:) = Gh(nx+1,:,:) Gh(:,2,:) = Gh(:,ny+1,:) do j=1,ny-1 do i=1,nx Gh(i,j,1) = cyh(i,j)*(My1(i,j)*r(i,j) + My2(i,j)*r(i,j+1)) Gh(i,j,2) = cyh(i,j)*(My1(i,j)*r(i,j)*u(i,j) + My2(i,j)*r(i,j+1)*u(i,j+1)) Gh(i,j,3) = cyh(i,j)*(My1(i,j)*r(i,j)*v(i,j) + My2(i,j)*r(i,j+1)*v(i,j+1)) + pyh(i,j) Gh(i,j,4) = cyh(i,j)*(My1(i,j)*r(i,j)*H(i,j) + My2(i,j)*r(i,j+1)*H(i,j+1)) end do end do do k=1,4 do j=2,ny-1 do i=2,nx-1 RHS(i,j,k) = - (Fh(i,j,k) - Fh(i-1,j,k))/dx - (Gh(i,j,k) - Gh(i,j-1,k))/dy end do end do end do end function RHS I have uploaded a screenshot at T = 1.0. As you can see on the right, there is build-up when it should just be periodic. The density is on a 128 x 128 resolution. Its not an optimal resolution but I'm doing it for speed/debugging purposes. EDIT: So I removed the boundary conditions and I get the same result. Furthermore, the arrays are unchanged when I remove the BC. Last edited by selig5576; April 24, 2017 at 12:42. |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
I think you are mixing up things. As explained in the earlier answers, you have two ways of enforcing periodicity, either on the fluxes OR on the state variables through ghost points.
If I understood correctly your indices, your physical domain is decomposed into finite volumes from 1 to nx and from 1 to ny. Your ghost cells are then located at 0, nx+1, 0, ny+1. And your faces go from 1 to nx+1, 1 to ny in the x direction and from 1 to nx, 1 to ny+1 in the y direction. Beforce calling the routine RHS, set the ghost cell boundary condition on the vector Q. Not Q1 ! That is to say on Qold and not Qnew. Q(0,:,: )=Q(nx,:,: ) Q(nx+1,:,: )=Q(1,:,: ) Q(:,0,: )=Q(:,ny,: ) Q(:,ny+1,: )=Q(:,1,: ) That's it. Then you construct your fluxes from face 1 to nx+1, 1 to ny in the x direction and from 1 to nx, 1 to ny+1 in the y direction. That way, in the x direction the flux computed at the face i=1 uses Q(0,:,: ) and Q(1,:,: ) and the flux computed at the last face nx+1 uses Q(nx,:,: ) and Q(nx+1,:,: ). And you do not need to set periodicity on Fh and Gh. Have a look to the book I mentionned, it is pretty well explained. |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi Francois,
You are indeed correct. 0, nx+1, and ny+1 are the ghost points. Upon reading the literature reference you gave me and the book by Leveque I implemented what I believe to be the correct way to set the boundary conditions. The problem I'm seeing when I print out the arrays and through the plots is that the boundary conditions are not being satisfied, i.e. when I remove the boundary conditions of Q I get the exact same result. I believe something else maybe wrong in my code. I've restructured some of my solver similar to what Leveque does for boundary conditions. Thank you for the patience and time. Code:
program EulerSolver
implicit none
integer :: i,j,k
integer, parameter :: nx = 129, ny = 129
real, parameter :: CFL = 0.5
real, parameter :: tEnd = 1.0
real, parameter :: gamma = 1.4000
real, dimension(nx,ny) :: x, y
real, dimension(0:nx+1,0:ny+1) :: r, u, v, p, E, H, c
real, dimension(0:nx+1,0:ny+1,4) :: Q, Q1, Q2, Qn
real, dimension(0:nx+1,0:ny+1,2) :: Eigenvalue
real, parameter :: xmin = 0.0, xmax = 1.0, ymin = 0.0, ymax = 1.0
real, parameter :: dx = (xmax-xmin)/real(nx-1, kind=8)
real, parameter :: dy = (ymax-ymin)/real(ny-1, kind=8)
real, parameter :: alpha = 3.0D+00/16.0D+00
real, parameter :: beta = 1.0D+00/8.0D+00
real, parameter :: onez = 1.0D+00
real :: t, sigma, pi, dt
pi = 3.14159265358979323846264338327950288419
sigma = 0.05/sqrt(2.0)
!Uniform grid
do j=1,ny
do i=1,nx
x(i,j) = xmin + (i-1)*dx
y(i,j) = ymin + (j-1)*dy
end do
end do
!Kelvin-Helmholtz initial conditions
do j=1,ny
do i=1,nx
if (y(i,j) > 0.25 .AND. y(i,j) < 0.75) then
r(i,j) = 2.0000
u(i,j) = 0.5000
else
r(i,j) = 1.0000
u(i,j) = -0.5000
end if
v(i,j) = 0.1*sin(4*pi*x(i,j))*(exp(-(y(i,j)-0.25)**2/(2*sigma**2)) + exp(-(y(i,j)-0.75)**2/(2*sigma**2)))
p(i,j) = 2.5000
c(i,j) = sqrt(gamma*p(i,j)/r(i,j))
E(i,j) = p(i,j)/(gamma-1) + (0.5D+00*r(i,j))*(u(i,j)**2 + v(i,j)**2)
H(i,j) = 0.5D+00*(u(i,j)**2 + v(i,j)**2) + c(i,j)**2/(gamma-1)
end do
end do
do j=1,ny
do i=1,nx
Eigenvalue(i,j,1) = abs(u(i,j)) + c(i,j)
Eigenvalue(i,j,2) = abs(v(i,j)) + c(i,j)
end do
end do
dt = CFL*min(dx/maxval(Eigenvalue(:,:,1)),dy/maxval(Eigenvalue(:,:,2)))
t = 0.D0
do while (t < tEnd)
do j=1,ny
do i=1,nx
Q(i,j,1) = r(i,j)
Q(i,j,2) = r(i,j)*u(i,j)
Q(i,j,3) = r(i,j)*v(i,j)
Q(i,j,4) = E(i,j)
end do
end do
Q(0,:,:) = Q(nx,:,:)
Q(nx+1,:,:) = Q(1,:,:)
Q(:,0,:) = Q(:,ny,:)
Q(:,ny+1,:) = Q(:,1,:)
!Shu TVD RK3
Q1 = Q + dt*RHS(Q, c, p, H)
Q2 = (3D+0/4D+0)*Q + (1D+0/4D+0)*Q1 + (1D+0/4D+0)*dt*RHS(Q1, c, p, H)
Qn = (1D+0/3D+0)*Q + (2D+0/3D+0)*Q2 + (2D+0/3D+0)*dt*RHS(Q2, c, p, H)
Q = Qn
r = Qn(:,:,1)
u = Qn(:,:,2)/Qn(:,:,1)
v = Qn(:,:,3)/Qn(:,:,1)
E = Qn(:,:,4)
p = (gamma-1)*(E - (0.5D+00*r)*(u**2.D0 + v**2.D0))
c = sqrt(gamma*p/r)
H = 0.5D+00*(u**2 + v**2) + c**2/(gamma-1)
t = t + dt
print *,'t=',t
end do
open(10,file='xcoord.dat',status='replace')
do i=1,nx
write(10,'(1000F14.7)') (x(i,j),j=1,ny)
end do
close(10)
open(10,file='ycoord.dat',status='replace')
do i=1,nx
write(10,'(1000F14.7)') (y(i,j),j=1,ny)
end do
close(10)
open(10,file='density.dat',status='replace')
do i=1,nx
write(10,'(1000F14.7)') (r(i,j),j=1,ny)
end do
close(1)
contains
function RHS (Q_in, c, p, H)
implicit none
real, dimension(0:nx+1,0:ny+1,4), intent(inout) :: Q_in
real, dimension(0:nx+1,0:ny+1), intent(in) :: c, p, H
real, dimension(0:nx+1,0:ny+1) :: Mxm, Mxp, Mym, Myp
real, dimension(0:nx+1,0:ny+1) :: pxp, pxm, pyp, pym
real, dimension(0:nx+1,0:ny+1) :: pxh
real, dimension(0:nx+1,0:ny+1) :: pyh
real, dimension(0:nx+1,0:ny+1) :: My1, My2, Myh
real, dimension(0:nx+1,0:ny+1) :: Mx1, Mx2, Mxh
real, dimension(0:nx+1,0:ny+1) :: Mxch, Mych
real, dimension(0:nx+1,0:ny+1,4) :: Fh
real, dimension(0:nx+1,0:ny+1,4) :: Gh
real, dimension(0:nx+1,0:ny+1) :: cxh
real, dimension(0:nx+1,0:ny+1) :: cyh
real, dimension(0:nx+1,0:ny+1,4) :: RHS
real, dimension(0:nx+1,0:ny+1) :: r, u, v, E
integer :: i, j, k
do j=1,ny
do i=1,nx
r(i,j) = Q_in(i,j,1)
u(i,j) = Q_in(i,j,2)/Q_in(i,j,1)
v(i,j) = Q_in(i,j,3)/Q_in(i,j,1)
E(i,j) = Q_in(i,j,4)
end do
end do
do j=1,ny
do i=1,nx-1
cxh(i,j) = sqrt(c(i,j)*c(i+1,j))
Mxch(i,j) = u(i,j)/cxh(i,j)
end do
end do
do j=1,ny
do i=1,nx
if (abs(Mxch(i,j)) >= 1) then
Mxp(i,j) = 0.5D+00*(Mxch(i,j) + abs(Mxch(i,j)))
Mxm(i,j) = 0.5D+00*(Mxch(i,j) - abs(Mxch(i,j)))
pxp(i,j) = 0.5D+00*(1.0D+00 + sign(onez,Mxch(i,j)))
pxm(i,j) = 0.5D+00*(1.0D+00 - sign(onez,Mxch(i,j)))
else
Mxp(i,j) = 0.25*(Mxch(i,j) + 1)**2 + beta*(Mxch(i,j)**2 - 1)**2
Mxm(i,j) = -0.25*(Mxch(i,j) - 1)**2 - beta*(Mxch(i,j)**2 - 1)**2
pxp(i,j) = 0.25*(Mxch(i,j) + 1)**2*(2 - Mxch(i,j)) + alpha*Mxch(i,j)*(Mxch(i,j)**2 - 1)**2
pxm(i,j) = 0.25*(Mxch(i,j) - 1)**2*(2 + Mxch(i,j)) - alpha*Mxch(i,j)*(Mxch(i,j)**2 - 1)**2
end if
end do
end do
do j=1,ny
do i=1,nx-1
Mxh(i,j) = Mxp(i,j) + Mxm(i+1,j)
Mx1(i,j) = 0.5D+00*(Mxh(i,j) + abs(Mxh(i,j)))
Mx2(i,j) = 0.5D+00*(Mxh(i,j) - abs(Mxh(i,j)))
pxh(i,j) = pxp(i,j)*p(i,j) + pxm(i+1,j)*p(i+1,j)
end do
end do
do j=1,ny-1
do i=1,nx
cyh(i,j) = sqrt(c(i,j)*c(i,j+1))
Mych(i,j) = v(i,j)/cyh(i,j)
end do
end do
do j=1,ny
do i=1,nx
if (abs(Mych(i,j)) >= 1) then
Myp(i,j) = 0.5D+00*(Mych(i,j) + abs(Mych(i,j)))
Mym(i,j) = 0.5D+00*(Mych(i,j) - abs(Mych(i,j)))
pyp(i,j) = 0.5D+00*(1.0D+00 + sign(onez,Mych(i,j)))
pym(i,j) = 0.5D+00*(1.0D+00 - sign(onez,Mych(i,j)))
else
Myp(i,j) = 0.25D+00*(Mych(i,j) + 1)**2 + beta*(Mych(i,j)**2 - 1)**2
Mym(i,j) = -0.25D+00*(Mych(i,j) - 1)**2 - beta*(Mych(i,j)**2 - 1)**2
pyp(i,j) = 0.25D+00*(Mych(i,j) + 1)**2*(2 - Mych(i,j)) + alpha*Mych(i,j)*(Mych(i,j)**2 - 1)**2
pym(i,j) = 0.25D+00*(Mych(i,j) - 1)**2*(2 + Mych(i,j)) - alpha*Mych(i,j)*(Mych(i,j)**2 - 1)**2
end if
end do
end do
do j=1,ny
do i=1,nx-1
Myh(i,j) = Myp(i,j) + Mym(i,j+1)
My1(i,j) = 0.5D+00*(Myh(i,j) + abs(Myh(i,j)))
My2(i,j) = 0.5D+00*(Myh(i,j) - abs(Myh(i,j)))
pyh(i,j) = pyp(i,j)*p(i,j) + pym(i,j+1)*p(i,j+1)
end do
end do
do j=1,ny-1
do i=1,nx
Fh(i,j,1) = cxh(i,j)*(Mx1(i,j)*r(i,j) + Mx2(i,j)*r(i+1,j))
Fh(i,j,2) = cxh(i,j)*(Mx1(i,j)*r(i,j)*u(i,j) + Mx2(i,j)*r(i+1,j)*u(i+1,j)) + pxh(i,j)
Fh(i,j,3) = cxh(i,j)*(Mx1(i,j)*r(i,j)*v(i,j) + Mx2(i,j)*r(i+1,j)*v(i+1,j))
Fh(i,j,4) = cxh(i,j)*(Mx1(i,j)*r(i,j)*H(i,j) + Mx2(i,j)*r(i+1,j)*H(i+1,j))
end do
end do
do j=1,ny-1
do i=1,nx
Gh(i,j,1) = cyh(i,j)*(My1(i,j)*r(i,j) + My2(i,j)*r(i,j+1))
Gh(i,j,2) = cyh(i,j)*(My1(i,j)*r(i,j)*u(i,j) + My2(i,j)*r(i,j+1)*u(i,j+1))
Gh(i,j,3) = cyh(i,j)*(My1(i,j)*r(i,j)*v(i,j) + My2(i,j)*r(i,j+1)*v(i,j+1)) + pyh(i,j)
Gh(i,j,4) = cyh(i,j)*(My1(i,j)*r(i,j)*H(i,j) + My2(i,j)*r(i,j+1)*H(i,j+1))
end do
end do
do k=1,4
do j=2,ny-1
do i=2,nx-1
RHS(i,j,k) = - (Fh(i,j,k) - Fh(i-1,j,k))/dx - (Gh(i,j,k) - Gh(i,j-1,k))/dy
end do
end do
end do
end function RHS
end program EulerSolver
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Centrifugal fan | j0hnny | CFX | 13 | October 1, 2019 13:55 |
| Wrong flow in ratating domain problem | Sanyo | CFX | 17 | August 15, 2015 06:20 |
| Problem with SIMPLEC-like finite volume channel flow boundary conditions | ghobold | Main CFD Forum | 3 | June 15, 2015 11:14 |
| PEMFC module + multiple periodic boundary conditions | vkrastev | FLUENT | 2 | December 22, 2014 04:15 |
| periodic boundary conditions fro pressure | Salem | Main CFD Forum | 21 | April 10, 2013 00:44 |