 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Mar 2017
Posts: 7
Rep Power: 9  |
I'm trying to add second order reconstruction based on the following Taylor expansions for the edge states from some advection notes:
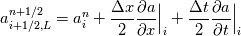 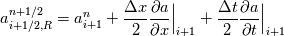 My plan is to apply these two equations to each of my conserved quantities (rho, rho*u, E) and use the spatial derivative of the corresponding quantity in the Euler equations (rho*u, rho*u*u+p, u(E+p)) for the time derivative. Like so 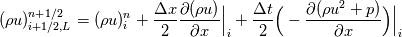 Then use something like centered differences for each of the spatial derivatives before converting back to the primitive variables for the Riemann solver. However, I've never seen it done like this so I wonder if this is wrong or there's a better way to implement piecewise linear reconstruction without using eigenvalues/characteristics? Edit: I'm using finite volume discretization. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I am not sure if you are trying to do a Lax-Wendroff like discretization...
However: 1) for non linear equations it requires much more terms 2) Being based on the Taylor expansion, that cannot be applied in case of non regular solutions such as those that can arise in Euler equations 3) you need to write the integral form and define a unique flux function on each face |
|
|
|

|
|
 |
| Tags |
| euler, godunov, piecewise linear method, plm, reconstruction |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Guide: Writing Equations in LaTeX on the CFD Online Forums | pete | Site Help, Feedback & Discussions | 27 | May 19, 2022 03:19 |
| SIMPLE Algorithm Finite Difference Equations: how to discretize and solve? | DA6righthand | Main CFD Forum | 0 | August 3, 2015 12:12 |
| modelling Differential equations in a udf | RikardMNorén | Fluent UDF and Scheme Programming | 2 | October 1, 2013 03:36 |
| Riemann invariants of adjoint equations of shallow water equations | zqb0929 | Main CFD Forum | 0 | March 15, 2012 00:54 |
| CFD governing equations | m.gos | Main CFD Forum | 0 | April 30, 2011 14:21 |