Home > Forums > General Forums > Main CFD Forum

Pressure correction for compressible gas

Updated Threads

Search this Thread

Prev

Previous Post

Next Post

Next

June 9, 2017, 05:08	Pressure correction for compressible gas	#1
lstum New Member Leonhard Schmalhorst Join Date: Nov 2015 Location: Munich, Germany Posts: 1 Rep Power: 0	Hi everyone, I'm trying to set up a solver in matlab for gas flowing through a fixed bed reactor. The equations i have are the momentum balances in axial and in radial direction and the mass continuity equation. So far, so good... My proceeding is as follows: Guess pressure field and velocity field Calculate axial velocity using the momentum balance in axial direction Calculate radial velocity using the momentum balance in radial direction Calcultate density field from continuity equation Calculate new pressure field using ideal gas law (I assume constant high temperatures, later i will solve the energy equation as well) Check for convergence If no convergence, go back to step 2 using the new calculated pressure field or only parts of it (e.g. $p_{new} = p_{old} + 0.5 (p_{new} - p_{old})$ ) Obviously, the steps 1-3 are the same as in nearly all algorithms. But since my algorithm does not work (oscillating residuals) i am not sure if steps 4 - 7 are correct. Does anyone has an advice for me? I'm thankful for every answer. Have a nice weekend, Cheers, Leo PS: Here are the equations i'm using: Momentum balance radial direction: 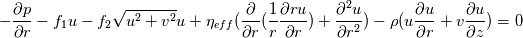$- \frac{\partial p}{\partial r} - f_1 u - f_2 \sqrt{u^2 + v^2} u + \eta _{eff} (\frac{\partial}{\partial r} (\frac{1}{r} \frac{\partial ru}{\partial r}) + \frac{\partial^2 u}{\partial r^2}) - \rho ( u \frac{\partial u}{\partial r} + v \frac{\partial u}{\partial z} ) = 0$ Momentum balance axial direction: 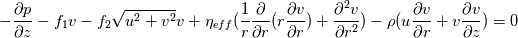$- \frac{\partial p}{\partial z} - f_1 v - f_2 \sqrt{u^2 + v^2} v + \eta _{eff} (\frac{1}{r} \frac{\partial}{\partial r} (r\frac{\partial v}{\partial r}) + \frac{\partial^2 v}{\partial r^2}) - \rho ( u \frac{\partial v}{\partial r} + v \frac{\partial v}{\partial z} ) = 0$ Continuity equation: 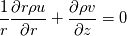$\frac{1}{r} \frac{\partial r\rho u}{\partial r} + \frac{\partial \rho v}{\partial z} = 0$ Ideal gas law: 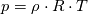$p = \rho \cdot R \cdot T$

Tags

compressible, fixed bed, gas, pressure correction

« Previous Thread | Next Thread »

Posting Rules
You may not post new threads You may not post replies You may not post attachments You may not edit your posts BB code is On Smilies are On [IMG] code is On HTML code is Off Trackbacks are Off Pingbacks are On Refbacks are On Forum Rules

Similar Threads
Thread	Thread Starter	Forum	Replies	Last Post
Wind tunnel Boundary Conditions in Fluent	metmet	FLUENT	6	October 30, 2019 12:23
SIMPLE algorithm does not converge when using old pressure (correction) values	andreasp	Main CFD Forum	3	February 9, 2016 21:18
Gas Diffusion and Pressure Distribution	Xuekun	Main CFD Forum	0	October 29, 2015 10:10
Using ideal gas law to simulate pressure decline	Björn Mattsson	FLUENT	5	September 5, 2005 04:03
Hydrostatic pressure in 2-phase flow modeling (long)	DS & HB	Main CFD Forum	0	January 8, 2000 15:00

All times are GMT -4. The time now is 13:59.