 |
|
|
[Sponsors] | |||||
potential flows, helmholtz decomposition and other stuffs |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Dec 2014
Posts: 5
Rep Power: 11  |
Hi I'm studying potential flow theory and I'd like too deeply understood this issue. I will present here the main lines of the theory in three points, as I have understood it, and some open questions for which I don't find an answer.
1) the equations that govern the behaviour of a steady, inviscid, incompressible and irrotational flow with conservative mass force field are: 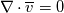 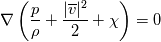 on the boundaries the only condition required is to impose the normal component of the velocity: 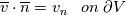 the hypothesis 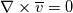 has been used to find out the momentuum equation in the form presented above and so is hidden inside it. Solving this system of equation we can find the solution where the field has been used to find out the momentuum equation in the form presented above and so is hidden inside it. Solving this system of equation we can find the solution where the field 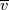 is uniquely defined while if we find a field of pressure is uniquely defined while if we find a field of pressure 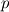 solution of the problem every other field solution of the problem every other field 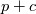 , where , where  is a constant value, is also a solution. is a constant value, is also a solution.2) Potential formulation. We can prove, using stoke's theorem, that every irrotational vectorial field defined over a simply connected domain is conservative. This allow us to rapresent the velocity as the gradient of a scalar potential field: 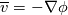 where the potential is defined with the following line integral where the path has to be contained inside the domain : 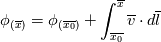 where 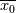 is a reference point inside the domain for which the value of the potential is usually considered as zero. This allow us to rewrite the initial set of equations as: is a reference point inside the domain for which the value of the potential is usually considered as zero. This allow us to rewrite the initial set of equations as: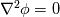 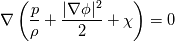 with the boundary condition: 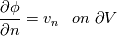 so in this case we are allowed to solve the laplace equation for  alone. Knowing the solution for alone. Knowing the solution for  we can find out the velocity field and also the pressure field from the momentuum equation that in this case can be solved indipendently. The solution of the laplace equation is a field we can find out the velocity field and also the pressure field from the momentuum equation that in this case can be solved indipendently. The solution of the laplace equation is a field  defined unless a constant defined unless a constant  ; every field ; every field 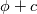 gives us the same field of velocity, but a pressure field defined unless a constant. gives us the same field of velocity, but a pressure field defined unless a constant.3) Helmholtz decomposition. Another well known result is that any kind of vectorial field defined in a simply connected domain can be decompose in the following way: 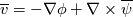 This decomposition is not unique because if we find two fields 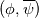 that fulfill the above statement every other couple of field that fulfill the above statement every other couple of field 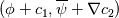 also fulfills the statement ( also fulfills the statement (  and and 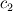 are arbitrary constants). It is also possible, using greens functions, to find out an explicit formulation for are arbitrary constants). It is also possible, using greens functions, to find out an explicit formulation for  and and 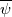 . For a three dimensional domain we have: . For a three dimensional domain we have:![\overline{v}_{(\overline{x})}=-\nabla \left[ \int_{V} \frac{\nabla '\cdot \overline{v}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d v' - \int_{\partial V} \frac{ \overline{v}_{(\overline{x'})} \cdot \overline{n}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d a' \right] \overline{v}_{(\overline{x})}=-\nabla \left[ \int_{V} \frac{\nabla '\cdot \overline{v}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d v' - \int_{\partial V} \frac{ \overline{v}_{(\overline{x'})} \cdot \overline{n}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d a' \right]](/Forums/vbLatex/img/bd7ab59b3e2e2a319a05d42fc72550aa-1.gif) ![+\nabla \times \left[ \int_{V} \frac{\nabla '\times \overline{v}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d v' + \int_{\partial V} \frac{ \overline{v}_{(\overline{x'})} \times \overline{n}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d a' \right] +\nabla \times \left[ \int_{V} \frac{\nabla '\times \overline{v}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d v' + \int_{\partial V} \frac{ \overline{v}_{(\overline{x'})} \times \overline{n}_{(\overline{x'})}}{|\overline{x}-\overline{x'}|} d a' \right]](/Forums/vbLatex/img/84ed17a02f399292ea5b916dd94d7332-1.gif) my interpretation of the former statement is that a vectorial field 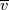 can be known if can be known if 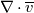 and and 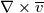 are known on the whole domain and moreover if are known on the whole domain and moreover if 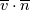 and and 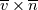 are known on the boundaries of the domain. are known on the boundaries of the domain.Now some questions. - dealing with point 1 and 2 In point one we can find a unique velocity field solving the whole system of equation while the pressure field remain undetermined unless a constant. In point two we can find a unique velocity field solving the sole laplace equation and the field of the scalar potential remain undetermined unless a constant. Here I see a sort of symmetry between the two cases. In this kind of problem the pressure is not the thermodynamic pressure ( because the flow is considered as incompressible) and some book adress the pressure as a lagrangian multipler, so a kind of mathematical element inside the problem. Is there some relation between the physical meaning of pressure and the physical meaning of the scalar potential? - dealing with point 1 and 3 In point three we have find out that a vectorial field 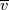 can be known if can be known if 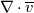 and and 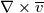 are known on the whole domain and moreover if are known on the whole domain and moreover if 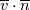 and and 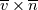 are known on the boundaries of the domain. In point one we have that are known on the boundaries of the domain. In point one we have that 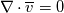 , , 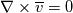 on the whole domain and also we have defined the normal component of the velocity on the boundaries; we don't have any information about the tangential component of the velocity on the boundaries, but we have the momentuum equation. So in this case the momentum equation seems to bring inside the problem the same amount of information as the knowledge of the tangential component of the velocity on the boundaries and moreover it bring inside the problem the pressure variable. Is it possible to reformulate the momentum equation in a way in which the former observation is showed in an explicit way? on the whole domain and also we have defined the normal component of the velocity on the boundaries; we don't have any information about the tangential component of the velocity on the boundaries, but we have the momentuum equation. So in this case the momentum equation seems to bring inside the problem the same amount of information as the knowledge of the tangential component of the velocity on the boundaries and moreover it bring inside the problem the pressure variable. Is it possible to reformulate the momentum equation in a way in which the former observation is showed in an explicit way?- dealing with point 2 and 3 In point two we have defined a scalar potential field starting from the assumption that the field of velocity is conservative, while in point three we have defined a scalar and a vectorial potential fields that are able to decopose a generic vectorial field. Is it possible to modify the explicit statement of the helmholtz decomposition under the assumption of solenoidal and irrotational field to reach the definition of the scalar potential presented in point two? I have waste some time on this issue but the two definitions look so different... How to reduce non-local integrals defined on a close surface to a line integral. The last question If we know that a velocity field is irrotational and solenoidal and moreover if we know the value of the normal component of the velocity on the boundaries what can we say about the tangential component of the velocity? It looks to be in some way constrained, but what is the explicit relation? I have tried to decompose the velocity on the boundaries using the relation: 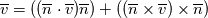 considering the first term as known and replacing the former statement inside 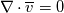 and in and in 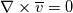 i thught to be able to find out a sort of constain for the value of the tangential component of the velocity, but my effort has been vain up to now. i thught to be able to find out a sort of constain for the value of the tangential component of the velocity, but my effort has been vain up to now.I hope someone can help me to clarify one or more of these issues. Thanks. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
What you are asking is intrinsic to the Helmholts-Hodge decomposition that is unique and orthogonal. Setting only one component is required to have the problem amthematically well posed. However, depending on the decomposition you can use either normal or tangential BC.s.
If you are interested in some theoretical details related to the NS equations for incompressible flow you can find them in https://www.researchgate.net/publica...ary_conditions |
|
|
|

|
|
 |
|
|