 |
|
|
[Sponsors] | |||||
Convergence order of three point central finite difference scheme |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
For example, when we solve simple 1D Poisson equation by finite difference method, why central difference scheme on uniform grid of form:
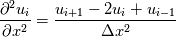 is second order method for solution convergence? I understand why approximation of first derivative is second order (and that second derivative is also second order because cancelation of first order truncation error term on uniform grid), but I donít understand why solution also converges with second order. Basically, this approximation is equivalent to fitting local quadratic (p=2) polynomial through three points which should theoretically yield third (p+1) order method? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
It is very simple to show the order of magnitude of the local truncation error, use two Taylor expansion around i (+h and -h), expressed up to fourth order terms |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
Thx FMDenaro, but let me explain in more details what is confusing me.
I used example of linear 1D Poisson equation (smooth exact solution) and compared convergence of few numerical methods with different order of basis (interpolation) functions. I used B-spline functions as basis functions. Order of convergence was determined for each method and each basis function by plotting graph "dx - error norm" in log-log scale and slope of the curve determines convergence order of method. Theoretically convergence order depends of polynomial order of basis function (Taylor series expansion), and for Galerkin method (classical FEM) there is full convergence order, i.e. if "p" is order of basis function than solution converges with order "p+1", while first derivative converges with order "p" and second derivative with order "p-1". For collocation method that is not case and there is reduction in convergence order. Now I'm trying to figure way. So I used also Finite difference method (FDM) with 3 point stencil CDS which is equivalent to approximation of second derivative by local polynomial of order p=2 (i.e. quadratic) and solution converges with order 2. By looking into Taylor expansion it is clear that first derivative approximation converges with order 2, and that second derivative converge also with order 2 (for uniform/symmetric grid and even-order polynomials as in this case). Now I'm looking for more detailed explanation why central difference scheme on three point stencil has same convergence order for solution as for first two derivatives. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
First, you are right when considering that a Lagrangian polynomial over three points is of degree 2 and therefore the accuracy of the interpolation of the function is O(h^3). A second order derivative is consequently a constant.
However, it is known that the FD second derivative has O(h^2) as it exploits the symmetry of the stencil that cancels some terms. The same as happens for the first derivative when apparently you have only 2 nodes and, hence the polynomial should be linear. That is like a fourth degree polynomial is used (5-points stencil, using also i+1/2 and i-1/2) for the second derivative. You can generalize this reasoning as shown here (sorry it is in italian) https://www.researchgate.net/publica...0686_Capitolo3 |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
And how can I derive formula for solution (not solutions derivatives) convergence order? And it still confuses me why is of order 2 when we are apparently using polynomial of degree 2 for approximation (so I would expect order 3).
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Sorry, your question is not clear to me. Try yourself to develop the local truncation espression for your problem.
|
|
|
|

|
|
|
|
|
#7 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Quote:
In my knowledge and test I have carried out quadratic polynomial gives third-order convergence only for interpolation. For the first derivative approximation, it will be (p) and for the second derivative, it will be (p-1) except symmetrical stencil where we can get order (p). The proof is straightforward from Taylors series expansion, assuming there is no stiffness in the solution that is the magnitude of higher derivate vanishes with the (grid size)^n. |
||
|
|

|
||
|
|
|
#8 | ||
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
Quote:
 and and 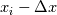 and sum them to get: and sum them to get: 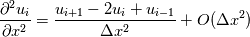 If we substitute this expression for example into Laplace equation we get:  This shows truncation error for approximation of Laplace equation by central finite difference operator. Now I'm trying to figure out how from here express convergence order of solution (i.e. discretization error). Can we simply express solution in central point as: 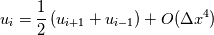 From here it seams that linear interpolation from two neighbor values should be 4th order accurate for this problem when we refine grid? However it is only second order accurate. What am I missing? Quote:
I have also solved 1D BVP governed by Poisson equation (also with cubic B-spline) and perform convergence analysis. In that case Galerkin formulation gives optimal convergence order (4/3/2), while collocation formulation gives convergence order (2/2/2). I found same results in the literature. Now I'm trying to figure why, and I decided to look what happens with FD method, and I'm not sure how to express convergences order of solution of BVP, and not convergence order of derivative approximation. |
|||
|
|

|
|||
|
|
|
#9 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
If u expand this expression in Taylors series you will get only second-order accurate. second order derivative term survive so u will be getting second order convergence.
|
|
|
|

|
|
|
|
|
#10 | |
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
Quote:
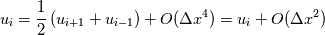 which doesn't have sense? |
||
|
|

|
||
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Be careful, you are confusing the "discretization error" from the "local truncation error".
Then, if yu consider the linear sistem A.x-q=0 and substitute an approximate solution you get A.xa-q=raand hence A.ea=-ra as you can see only if ||A|| =O(1) you get that the error is of the same magnitude order of the residual. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
||
|
|

|
|
|
|
|
#13 | |
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
Quote:
I assume that here ea is discretization error, and ra is residual because of truncation error? And how can I express convergence order of discretization error if I know order of highest truncated term? |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
The key is to understand that you are discretizing the Laplace equation using second order approximation for the differential operators that is (2D problem with constant mesh size h) d2fe/dx^2+d2fe/dy^2-[-4*fe(i,j)+fe(i+1,j)+fe(i-1,j)+fe(i,j+1)+fe(i,j-1)]/h^2= LTE of O(h^2) where fe=fe(x,y) is the exact solution (I simplified fe(xi,yj) as fe(i,j)). If you have that fe(x,y) is a known analytical function in your test, you conversely check the convergence of (fn is the vector of the numerical solution: (fe -fn)= discretization error |
||
|
|

|
||
|
|
|
#15 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Maybe I am not understanding the question, but let me try to answer. If you have a second order approximation for u'' then your solution will typically converge on the order of 2. In steady state, such as solving u'' = f, you only worry about your discretization method accuracy. In a transient problem you have to worry about your scheme being consistently second order in space and time. For example, BTCS is second order in space but only first order in time. Crank-Nicholson is second order in time and in space.
There are situations where, despite having second order discrete operators, you might only give a first order solution. For example, if you have discontinuous data, this can affect the accuracy of your solution. I would look at the book of Leveque for more on error analysis of discrete differential operators. |
|
|
|

|
|
|
|
|
#16 | |||
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
Quote:
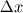 and then calculate convergence order. and then calculate convergence order. If we use classical Galerkin FEM and quadratic Lagrangian polynomials we will get that solution converges by order 3. If we differentiate numerical solution and compare with exact first derivative of solution we will get that 1st derivative converges by order 2, and 2nd derivative will converge with order 1. It means that in Galerkin FEM convergence order depends directly on order of Lagrangian polynomial (I am assuming ideal case when solution is sufficiently regular). Now I'm trying to relate this with convergence of FDM. Apparently we are dealing with quadratic polynomial (or even of degree 4; because of symmetry for second derivative approximation) but our FDM is only 2nd order method. I can't figure why. I know that collocation method for same basis function will have reduced order when compared with Galerkin. Is there some order reduction in FDM because its nature of approximation? Quote:
Quote:
|
||||
|
|

|
||||
|
|
|
#17 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Be careful on the fact that in variational formulation you introduce the integration and thus one derivative disappears. Therefore, your shape function is never used for a second derivative.
|
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
If you have a second order discrete operator, especially in the case of FDM, your solution accuracy depends on the accuracy of your discretization process. To convince yourself, do a log-log plot in the L2 error (for example) of a variety of resolutions.
|
|
|
|

|
|
|
|
|
#19 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Quote:
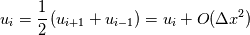 In this expression, you could think that while expanding in Taylors series second order term survive, but Laplace equation says the second derivative is zero so it could give fourth order but unluckily numerical method approximate the solution. Numerically we didn't ensure 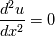 so it will not give fourth order accuracy. A few years ago I tried this in one assignment at that time I am also got second-order accuracy. so it will not give fourth order accuracy. A few years ago I tried this in one assignment at that time I am also got second-order accuracy. Anyway, I like this way of thinking about this simple problem! Last edited by arungovindneelan; November 11, 2017 at 10:30. |
||
|
|

|
||
|
|
|
#20 |
|
New Member
Luka Malenica
Join Date: Feb 2017
Location: Split, Croatia
Posts: 8
Rep Power: 9  |
My opinion is that polynomial order determines theoretical (maximum) order of approximation. Differential operator (i.e. order of PDE/ODE) should affect only accuracy of the approximation and not the order. From results what I see its seems that that formulation/method can reduce order of method but I don't know how to verify/prove it.
One more thing that confuses me here. If we consider unsteady convection equation and discretized both spatial and temporal derivatives with forward (or backward) finite difference our method is first order accurate both in space and time. Both terms are derived by using first two terms from Taylor series (linear approximation) which implies second order method when we consider solution (not derivative) convergence order. Moreover we know that Euler temporal discretization is locally (if we consider single time step) 2nd order accurate, and that loses one order because accumulation of error during time (multiple time steps). Why then is spatial discretization only 1st order and not 2nd order accurate? |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Code verification of second order scheme | kmandar | SU2 | 0 | June 26, 2016 10:28 |
| AUSM scheme ? Central Scheme | boling | Main CFD Forum | 7 | January 7, 2016 02:41 |
| High-order finite difference scheme for incompressible Navier Stokes equation | novan tofany | Main CFD Forum | 2 | April 5, 2012 06:34 |
| Force can not converge | colopolo | CFX | 13 | October 4, 2011 22:03 |
| Definition of limiter function for central dirrerencing scheme | sebastian_vogl | OpenFOAM Running, Solving & CFD | 0 | January 5, 2009 11:08 |