 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: May 2017
Posts: 10
Rep Power: 9  |
Hello Everyone,
I want to calculate the integral length scale directly from the energy spectrum. According to Wiki (https://en.wikipedia.org/wiki/Integral_length_scale) this can be done via 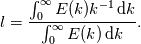 But I am working on 2D-flows and I have reason to suspect, that this formula should include a factor of 2 in this case, though I couldn't find anything about this. Does anyone know whether there is indeed a factor of 2 or if I am mistaken? Thanks a lot and greetings |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
What is your specific reasoning for the factor 2 in 2D?
Actually, my opinion is that any evalution of the integral lenght is for the order of magnitude, so that a factor of 2 would not change so much. See https://www.researchgate.net/publica...Numerical_Data |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: May 2017
Posts: 10
Rep Power: 9  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
These formulae look quite arbitrary. What is the result for 3D?
|
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: May 2017
Posts: 10
Rep Power: 9  |
I'm sorry, but I do not understand. What do you think is arbitrary?
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I think you could start by the general definition in terms of the integral of the autocorrelation, considering that spectra and correlation are related each other by direct/inverse Fourier transformation.
But in general the determination of the integral scale is somehow still debated, as you can see for example here http://www.turbulence-online.com/Pub...apers/WG02.pdf |
|
|
|

|
|
 |
| Tags |
| integral length scale, length scale, two dimensional |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| to determine Integral length scale in Fluent | raunakjung | FLUENT | 3 | February 7, 2017 09:03 |
| Turbulence length scale and integral length scale | rizhang | CFX | 2 | April 22, 2016 07:22 |
| Integral length length scale | nasir.iitd | FLUENT | 2 | June 11, 2014 08:37 |
| Integral Length Scale vs Turbulent Length Scale | Scott Nordsen | FLUENT | 2 | January 20, 2014 01:17 |
| Von Karman Integral Length Scale | Txingurri | Main CFD Forum | 0 | May 2, 2002 12:05 |