[mtaskin]

Hi,
I have been asked to perform Gauss-Seidel methods(explicit and implicit) and Line Successive Over-relaxation method on a linear 2-D Elliptic Equation. So i wrote a fortran code and now i have to compare my results with exact results in a reference textbook. The problem is the absolute errors are quite high(sometimes 20%).


So i checked my code multiple times but there is no error. Than i realized, my indicated step size was 0.02 ft where the textbook uses 0.05 ft. The funny thing, when i run the code with textbook step size(larger step size) i get perfect match with the result. So i am confused and started looking for an answer. Here is what i did so far;


- I discretized BS(Backward space) rather than CS(central space) but errors are getting larger which is not surprising(first order and all stuff considered)
- I derived modified equation and found out that artificial viscosity is dominating error. But dont you think 20% absolute error is quite high for artificial viscosity alone?
- I thought i did something wrong in modified equation and decided to run my code with double precision, in case round-off error is dominating. The same phenomena happens.
- I theorized that textbook authors made a mistake by publishing unconverged solution but relative error control sequence shows it is converged result(it was a low possibility anyways)
- I know i can produce lower accuracy with lower step sizes for non linear equations but this one is linear so this is not the case, i eliminated this reason pretty quickly.



So i ran out of ideas. I know there are lots of experienced people here. Can you think of any possible reason? Even a little hint would be appreciated. Thank you in advance


Best regards,
mtaskin

[FMDenaro]

What kind of problem are you solving? For elliptic problems there is no reason to use first order upwinding! Then, the GS or SOR procedure is an iterative process, the quality of your final solution depends on the stopping criterium. How do you control it?


I suggest to post all the details of your PDE problem and the figures of the convergence error slope.

[mtaskin]

Originally Posted by FMDenaro

What kind of problem are you solving? For elliptic problems there is no reason to use first order upwinding! Then, the GS or SOR procedure is an iterative process, the quality of your final solution depends on the stopping criterium. How do you control it?


I suggest to post all the details of your PDE problem and the figures of the convergence error slope.

Hi,
Thanks for the reply and sorry. I thought i should keep it brief but i guess it wasnt explaining enough.



I didnt use first order upwinding but as far as i understand central differencing scheme can also lead artificial viscosity. Am i wrong in that sense? if i am then i did something really wrong when deriving modified equation. If there is a reference for deriving elliptic equation's modified equation, i would really appreciate it.
As for the details,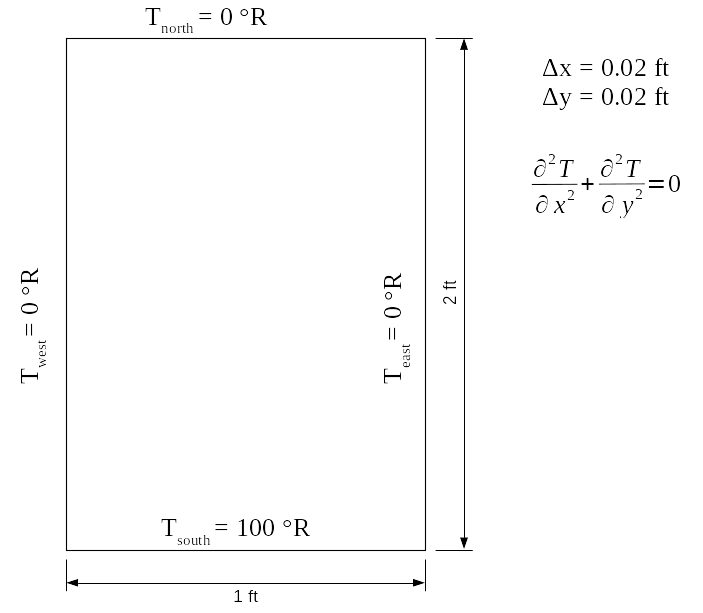



The attached figure is schematic representation of the problem i need solve with Point Gauss Seidel, Line Gauss Seidel and LSOR. I wrote a Fortran code for it and i used the same control sequence for all of them which is relative error.

do 65 k = 1,1000
       do 66 i = ny-1,2,-1
          do 67 j = 2, nx-1

             if (j == nx-1) then
                D(j) = -beta**2*(Told(i-1,j) + Tnew(i+1,j)) - Tnew(i,j+1)
             else if (j == 2) then
                D(j) = -beta**2*(Told(i-1,j) + Tnew(i+1,j)) - Tnew(i,j-1)
             else
                D(j) = -beta**2*(Tnew(i+1,j)+Told(i-1,j))
             end if

             H(j) = c/(b-a*H(j-1))
             G(j) = (D(j)-a*G(j-1))/(b-a*H(j-1))
             Tnew(i,j) = -H(j)*Told(i,j+1) + G(j)
             rerr(i,j) = abs(Tnew(i,j)-Told(i,j))/Tnew(i,j)*100
67        end do
66     end do
       Told = Tnew

       if (all(rerr <= emax)) then
          exit
       end if
65  end do

What it does, calculates the relative error for each vertex(or node) and when each element is less than maximum error limit, the code exits from the loop(emax = 0.5%). This particular code is for line gauss seidel with Tridiagonal matrix algorithm. To clarify relative error i used is defined in Steven Chapra's book;



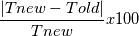I didnt post all the code since it is long but what i did basically, discretized the elliptic equation with central space differencing scheme and then derive the equations for respective methods.


As for the rate of convergence graphs, i am afraid i did not store error for each iterations since diagonal dominance is present. Also i thought, if it does not convergence with 1000 iterations, there must be some mistake in the code. So i have only the last error matrix that i have(to save time and space). But i do understand the suggestion behind it. So i will revise the code to give me errors for each step but i figure it will take time.



Best regards,
mtaskin

[Simbelmynë]

You state that you compare the results with "exact" results from the textbook. Then you state that the textbook uses a step-size of 0.5 ft, which indicates that the authors of the book have presented a numerical solution.


1. Please confirm that the solution is indeed exact. If not, then you might be comparing your results to a non mesh independent solution.


2. Try playing around with the convergence criterion (you have set a maximum of 1000 iterations, are you sure the solution converge before that?)



3. Change the east/west boundaries to zero flux and confirm that you get a linear profile between the south/north walls.

[mtaskin]

Hi,


Thank you for the answer and advice you gave me. It made me double check everything.



1) I checked. There are two result in the textbook. One of them is Gauss-Seidel Method results with 0.05ft step size and the other one is exact results with analytical solution.


2) I did play with the criterion as you asked. I have been keeping an eye on iteration count and there are no changes unless i change maximum allowable error(it converges before 1000 iterations, that is why i have if statement in the code). I also graphed convergence graphs and there is no indication of converge and diverge again. It seems everything goes smoothly according to relative error logs.


3) Yeah i get a linear profile when i set zero flux on east and west boundary.



Yesterday i had a chance to ask this occurrence to some of my friends,instructors but they seemed confused too. I think i will change my code and how it works. Maybe despite all my cross-checking, i am skipping some logical error. Since i almost checked everything, that is the only logical explanation. As for me getting perfect match with 0.05ft step sizes, i will count it as 'coincidence' until i get new possible explanations.



Thank you for your guidance,advice and help. Please consider the thread is closed and solved.(new idea entries still welcome tough)



Best regards,
mtaskin

[FMDenaro]

You are wrong, the second order central discretization for the second derivative has a local truncation error where fourth order derivative appears. This is not a numerical viscosity

[mtaskin]

Hi,
Thank you for the answer. You were right. I clarified how to derive modified equation in such cases yesterday. My mistake was trying to expand taylor series for iteration term like it was time term(in my defense my instructor told me multiple times that in essence they behave alike. Yesterday i have been 'reminded' that the thing he said was analogy for not to confuse us. LOL) I got an earful for that.


Best regards
mtaskin