 |
|
|
[Sponsors] | |||||
Difference between diffusion, dissipation and dispersion in physical and numerical |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
Hi,
I am really confused about the difference between diffusion, dissipation and dispersion in physical and numerical sense. (Following are my understandings) In physical sense: - Diffusion is like "spread out". The parameter spread out the space; - Dissipation is like the parameter is "gone". Like the momentum transfer to internal energy or heat, the momentum is "lost". - I've never encountered dispersion in physical sense, so I guess there is no dispersion in this way. In numerical sense: - Diffusion & dissipation are the same (I am not sure). - Dispersion is the oscillations in the solution. =============================================== I found this earlier thread talking about the similar topic Numerical diffusion/dispersion/dissipation Here says, in numerical sense, diffusion = dissipation + dispersion. However, some people I had talked to take dispersion as error in phase (what?). Now I am lost. Is there any precise definitions for these terminologies? |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
|
Diffusion refers to a phenomenon where some quantity spreads out in space as time goes on.
Dissipation is used to refer to loss of energy. The effects are related. If you consider the heat equation 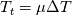 and start with an initial condition with high temperature in some small region, then the temperature distribution spreads out. This would be called diffusion. If you calculate 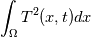 this quantity will decrease with time. So there is a loss of energy. (This is not really energy in physical sense if T is temperature, you can substitute velocity here). Both are caused by the Laplacian term. If something spreads out, its square integral will probably decrease. Dispersion is related to wave phenomena. For a linear wave equation 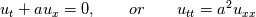 you can resolve the solution into fourier modes. Then each mode will travel at the same speed. We say such equations are non-dispersive. These two equations are also non-dissipative. For smooth solutions with periodic bc, they conserve all integrals of the form 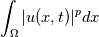 An equation like 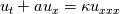 would have solutions whose fourier modes travel at different speed depending on  and wave number. We say these equations exhibit dispersive behaviour. and wave number. We say these equations exhibit dispersive behaviour.We observe these phenomena at the level of pde and we can map them to the behaviour of numerical schemes. If you solve a non-dissipative and non-dispersive pde with a numerical scheme, you want the numerical solutions to be non-dissipative and non-dispersive. Sadly this is not possible since numerical solutions will exhibit these behaviours even if the exact solution does not. Then we say that the numerical scheme is dissipative and/or dispersive and the interesting thing is to design schemes which atleast minimize these effects which are not present in the exact solution. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Praveen provided a good answer, I just suggest to see the numerical effects of diffusion and dispersion by using the modified wavenumber analysis for the linear wave equation discretized by first and second order FD in space.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Joern Beilke
Join Date: Mar 2009
Location: Dresden
Posts: 507
Rep Power: 20  |
Dispersion is sometimes used as the sum of convection + dissipation.
So you always have to ask, how these words are used. Never ever rely on a general definition. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
|
Quote:
I still have some questions: - diffusion like "spread-out", dissipation like "loss". Then how we recognize if a numerical scheme is "diffusive" or "dissipative"? By taking integral and see if the variable decreases? If it decreases, then it's dissipative; if not, then it's diffusive. Am I right? - as for the Fourier representation, I have seen people using different formula: some use combination of harmonic functions in space and exponential in time (something like sin(x)exp(t) + cos(x)exp(t)), while some use purely exponential (something like  ). Which one would you recommend for this analysis? ). Which one would you recommend for this analysis?- Is there anything used for describe the phase error? |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
I am familiar with the modified wave number. I can understand the deficiency in modified wave number can lead to dispersion. But how does it cause diffusion?
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
|
||
|
|

|
|
|
|
|
#8 |
|
Senior Member
Joern Beilke
Join Date: Mar 2009
Location: Dresden
Posts: 507
Rep Power: 20  |
||
|
|

|
|
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
You have simply to start with the exact solution of the linear wave equation and compare the real and imaginary part to the exact wavenumber. If you are familiar with the modified wavenumber analysis you could be able to follow this text (written in italian fro my CFD students) that explain the character (numerical viscosity and dispersion) of the numerical errors for several FD formulas |
||
|
|

|
||
 |
| Tags |
| diffusion, dispersion, dissipation, numerical, physical |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Numerical dissipation and dispersion | hityangsir | Main CFD Forum | 9 | April 15, 2015 00:58 |