 |
|
|
[Sponsors] | |||||
Interpretation of Spalding's viscosity damping coefficient |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Jan 2019
Posts: 7
Rep Power: 7  |
According to Spalding's law of the wall we have
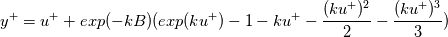 leading to 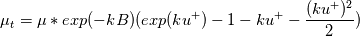 , which can be interpreted as a damping function applied to the viscosity. , which can be interpreted as a damping function applied to the viscosity. How does this damping function behave (or should behave) as 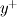 becomes large. Also up till what values of becomes large. Also up till what values of 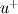 does the expression for does the expression for 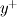 hold? It seems that in order for the latter to be equal to, say, 100, a negative value for the former is needed. How is this possible? hold? It seems that in order for the latter to be equal to, say, 100, a negative value for the former is needed. How is this possible?
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
Quote:
![y^+ = u^+ + e^{-kB}\left[e^{ku^{+}}-\sum_{i=0}^N \frac{\left(ku^+\right)^i}{i!}\right] y^+ = u^+ + e^{-kB}\left[e^{ku^{+}}-\sum_{i=0}^N \frac{\left(ku^+\right)^i}{i!}\right]](/Forums/vbLatex/img/567c4493c7d217a1a2c2142ea87576e4-1.gif) while the turbulent viscosity ratio implied by equilibrium wall model is: 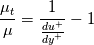 From the first one you can obtain by straightforward differentiation: ![\frac{dy^+}{du^+}=1+ke^{-kB}\left[e^{ku^+}-\sum_{i=1}^N \frac{\left(ku^+\right)^{i-1}}{\left(i-1\right)!}\right] = 1+k\left[\left(y^+-u^+\right)+e^{-kB}\frac{\left(ku^+\right)^N}{N!}\right] \frac{dy^+}{du^+}=1+ke^{-kB}\left[e^{ku^+}-\sum_{i=1}^N \frac{\left(ku^+\right)^{i-1}}{\left(i-1\right)!}\right] = 1+k\left[\left(y^+-u^+\right)+e^{-kB}\frac{\left(ku^+\right)^N}{N!}\right]](/Forums/vbLatex/img/eb221d9fe3f2b72debf7b4f8d6842650-1.gif) where the original law has been used again in the last passage. It follows that: ![\frac{\mu_t}{\mu}=k\left[\left(y^+-u^+\right)+e^{-kB}\frac{\left(ku^+\right)^N}{N!}\right] \frac{\mu_t}{\mu}=k\left[\left(y^+-u^+\right)+e^{-kB}\frac{\left(ku^+\right)^N}{N!}\right]](/Forums/vbLatex/img/66a5129927b3e129d2d7bf720d14e785-1.gif) Note that 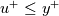 , and this is a damping just approaching the viscous sublayer (where , and this is a damping just approaching the viscous sublayer (where 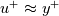 ). But even in that case, talking of damping is misleading, it is just that the turbulent viscosity is nondimensionalized by the molecular viscosity. ). But even in that case, talking of damping is misleading, it is just that the turbulent viscosity is nondimensionalized by the molecular viscosity.
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Jan 2019
Posts: 7
Rep Power: 7  |
Quote:
However, how would this function behave on the interval 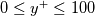 ? I mean, we would expect the damping ( or ratio for that matter) to become large as we approach ? I mean, we would expect the damping ( or ratio for that matter) to become large as we approach 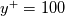 . But in the expression . But in the expression 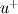 is found. The only way to get rid of that is to substitute either is found. The only way to get rid of that is to substitute either 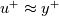 or or 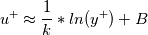 . But then the idea of one expression for the whole region is lost, right? . But then the idea of one expression for the whole region is lost, right?
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
|
Quote:
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
|
Let me state it more clearly: Spalding's law of the wall is not a relation valid for any law of the wall (i.e., any form of u+), so that you just put something in u+ and expect it to be valid.
It is a law of the wall, just expressed in reverse form (I don't have the original paper so I can't say where this comes from), as u+ in function of y+. That's it. |
|
|
|

|
|
|
|
|
#6 | |
|
New Member
Join Date: Jan 2019
Posts: 7
Rep Power: 7  |
Quote:
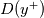 ), whereas the 'damping function' we are considering is now a function of the nondimensionalized wall distance and velocity( ), whereas the 'damping function' we are considering is now a function of the nondimensionalized wall distance and velocity(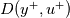 ). But I want to get insight in how this function behaves with ). But I want to get insight in how this function behaves with 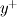 . Since . Since 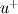 is a function of is a function of 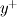 , I looked for a proper substitution such that I can see the behavior. , I looked for a proper substitution such that I can see the behavior.
|
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
|
Quote:
Here it is a simple MATLAB script to have all such quantities for N=4: %U is the independent variable in Spalding Law of the Wall u=(0:0.01:30); %Original Spalding constants k=0.4; B=5.5; c=exp(-k*B); %Original Spalding Formula y=u+c*(exp(k*u)-1-k*u-(k*u).^2/2-(k*u).^3/6-(k*u).^4/24); %Resulting viscosity ratio mutmu=k*(y-u+c*(k*u).^4/24); %Resulting wall damping D=1-u./y+((c/24)*(k*u).^4)./y; %Velocity plot figure() semilogx(y,u) %Turbulent viscosity ratio plot loglog(y,mutmu) %Damping plot semilogx(y,D) |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,779
Rep Power: 71    |
Quote:
If I remember correctly, the Spalding's law is a proposal to express the law of wall u+(y+) in a unique expression (but without taking into account the pressure gradient) in all the regions. I don't think that is directly related to a dumping viscosity concept. Have a look here https://ntrs.nasa.gov/archive/nasa/c...9990081113.pdf |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
Quote:
|
|
|
|

|
|
|
|
|
#10 | |
|
New Member
velkon123
Join Date: Jan 2020
Posts: 14
Rep Power: 6  |
Thank you for this matlab code, the only thing I do not really get is how to go from the equation of eddy viscosity to its damping factor equation. Do you also know in addition how to derive the damping factor for the mixing length as it would follow out of Spaldings law?
Quote:
|
||
|
|

|
||
|
|
|
#11 | |
|
Senior Member
|
Quote:
![\frac{\mu_t}{\mu}=k\left[\left(y^+-u^+\right)+e^{-kB}\frac{\left(ku^+\right)^N}{N!}\right] \frac{\mu_t}{\mu}=k\left[\left(y^+-u^+\right)+e^{-kB}\frac{\left(ku^+\right)^N}{N!}\right]](/Forums/vbLatex/img/66a5129927b3e129d2d7bf720d14e785-1.gif) then the last step to obtain D, the damping factor for the mixing length in the Spalding formulation, is to simply collect y+ out of the square parenthesis in the formula above, resulting in: ![\frac{\mu_t}{\mu}=k y^+\left[\left(1-\frac{u^+}{y^+}\right)+\frac{e^{-kB}}{y^+}\frac{\left(ku^+\right)^N}{N!}\right] = k y^+ D\left(y^+,u^+\right) = l^+ D\left(y^+,u^+\right) \frac{\mu_t}{\mu}=k y^+\left[\left(1-\frac{u^+}{y^+}\right)+\frac{e^{-kB}}{y^+}\frac{\left(ku^+\right)^N}{N!}\right] = k y^+ D\left(y^+,u^+\right) = l^+ D\left(y^+,u^+\right)](/Forums/vbLatex/img/dcfa27c9eaf2fb1ded5dc6438b0a7913-1.gif) So, D (the square parenthesis), as derived above, is the damping factor for the mixing length underlying the Spalding formulation. I can say so because I first derived mut/mu from the Spalding formulation, and then expressed it as a mixing length (l^+) times a damping term (D). So, the general approach is: you have a mut/mu formulation, you collect ky^+, what remains is some factor with respect to the mixing length. If this factor is really damping just depends from the original mut/mu model. Often this damping factor is just introduced artificially (that is the mut/mu formulation is built from a mixing length and a purposedly designed damping factor). Note that I bravely divided by y+ wherever I needed; I knew I could do this because I have u+ at numerator in those terms, and the ratio is finite for y+ going to 0 (at least it is within the formulation adopted). |
||
|
|

|
||
|
|
|
#12 |
|
New Member
velkon123
Join Date: Jan 2020
Posts: 14
Rep Power: 6  |
Aha thank you, so if I understand well the damping factor for the eddy viscosity is the same as for the mixing length? Or is there a different damping factor for the eddy viscosity following from Spaldings Law?
Quote:
|
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
|
Quote:
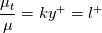 and, as you see, it has no damping factor at all. While it has the correct form for the logarithmic layer, it is known to be wrong in the viscous sublayer, where the turbulent viscosity is known to scale as 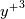 . So people have added to it empirical damping factors to make it scale correctly. For example, the Van Driest one has the general following form: . So people have added to it empirical damping factors to make it scale correctly. For example, the Van Driest one has the general following form:![D\left(y^+,A^+,n,m\right) = \left[1-e^{-\left(\frac{y^+}{A^+}\right)^n}\right]^m D\left(y^+,A^+,n,m\right) = \left[1-e^{-\left(\frac{y^+}{A^+}\right)^n}\right]^m](/Forums/vbLatex/img/85ff0c5ab4f1f0456cce04a3883a9eb9-1.gif) where m=2 gives the correct near wall scaling. Then the resulting model is built, empirically (as opposed to derived) as: 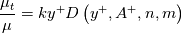 Now, in contrast to this line of thinking, there are models that don't formally start from a mixing length hypothesis. The one of Spalding is such a model. Another example is the Musker one (which is very similar to the one underlying the Spalart-Allmaras model near the wall): 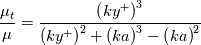 In these cases you don't formally have a mixing length and a damping factor, but you can always collect 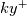 , which is the mixing length, and whatever remains is, as a matter of fact, the underlying damping factor. We already did this exercise for the Spalding model; it is much simpler for the Musker one: , which is the mixing length, and whatever remains is, as a matter of fact, the underlying damping factor. We already did this exercise for the Spalding model; it is much simpler for the Musker one:![\frac{\mu_t}{\mu}= \frac{\left(ky^+\right)^3}{\left(ky^+\right)^2+\left(ka\right)^3-\left(ka\right)^2} = k y^+ \left[\frac{\left(ky^+\right)^2}{\left(ky^+\right)^2+\left(ka\right)^3-\left(ka\right)^2}\right] = k y^+ D\left(y^+,k,a\right) \frac{\mu_t}{\mu}= \frac{\left(ky^+\right)^3}{\left(ky^+\right)^2+\left(ka\right)^3-\left(ka\right)^2} = k y^+ \left[\frac{\left(ky^+\right)^2}{\left(ky^+\right)^2+\left(ka\right)^3-\left(ka\right)^2}\right] = k y^+ D\left(y^+,k,a\right)](/Forums/vbLatex/img/389c67208498a7f01f80ed7ed8c892fd-1.gif) As for the Spalding model, it turns out that the damping factor we derived from the Musker model is actually a damping. So, to answer your question, mixing length actually means just a 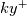 scaling for the turbulent viscosity and, by definition, it has no damping factor. People have added damping factor to the mixing length, empirically, to actually make it well behaved in the viscous layer. This is one way of formulating the near wall viscosity model (i.e., starting from a mixing length times a damping factor.) There are, however, other means of doing it; in this case you don't explicitly start from the mixing length and the damping factor but, usually, they are easily obtained by just collecting the correct terms as I have shown you for two such models (Spalding and Musker). scaling for the turbulent viscosity and, by definition, it has no damping factor. People have added damping factor to the mixing length, empirically, to actually make it well behaved in the viscous layer. This is one way of formulating the near wall viscosity model (i.e., starting from a mixing length times a damping factor.) There are, however, other means of doing it; in this case you don't explicitly start from the mixing length and the damping factor but, usually, they are easily obtained by just collecting the correct terms as I have shown you for two such models (Spalding and Musker).
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Vertical Damping on OpenFoam (lambda coefficient) | OtavioDuarte | OpenFOAM | 2 | April 23, 2022 01:45 |
| driftFluxFoam viscosity model modification problem | dleduc | OpenFOAM Programming & Development | 15 | October 1, 2018 09:37 |
| stiffness and damping coefficient | Seonjin | CFX | 0 | December 8, 2006 00:10 |
| Two-Phase Buoyant Flow Issue | Miguel Baritto | CFX | 4 | August 31, 2006 12:02 |
| Damping coefficient | Yemelong Edgard Constand | Main CFD Forum | 0 | December 4, 2000 12:45 |