[granzer]

I understand what an implicit and explicit form of finite-difference (FD) discretization for the transient heat conduction equation means. But I am not able to understand if it is possible to categorize the discretization of steady state heat conduction equation (without a source term, i.e Laplace equation) as implicit or explicit scheme as well?(or is it just implicit form of discretization as we use iterative solvers?)

Whenever I try to understand the meaning of explicit an implicit solvers, the notes and other resources always explain them using a (transient) time-varying equation. According to such resources For a transient equation if the solution for the next time step is given in terms of current time step values (which we already know, either by initial condition or by previous calculation) it is called as an Explicit solution, and it could be solved for directly without forming a system of equation. If the solution for next time step value is given in terms of current time step values (which we know) and next time step values (which we don't know) it leads to an implicit solution and this gives us a system of equations which is solved for by iterative solvers.

My confusion is, if we take a steady state equation there are no time steps involved (so there is no current and next time step) so what would be an explicit and implicit solution? and why would an explicit solution require an iterative solver as they can be solved for directly?

[LuckyTran]

The difference between explicit and implicit time-stepping as you already know is whether you are doing purely arithmetic or solving a system of equations. Although I'm about to spoil the beans, what do you think a steady state solver does exactly? How would you perform the spatial discretization... Think about it...


In FVM: steady state solvers are often transient solvers with a disguise.

Originally Posted by granzer

My confusion is, if we take a steady state equation there are no time steps involved (so there is no current and next time step) so what would be an explicit and implicit solution? and why would an explicit solution require an iterative solver as they can be solved for directly?

First. Forget that an iterative solver is involved. In the explicit case, you advance the solution in time a certain amount. Here there is no real solver because it's just purely arithmetic.


In the implicit case, you have a system of equations and this system of equations needs to be solved somehow. Suppose you have some heavenly algorithm contained in a black box that solves the system of equations exactly all the time and never diverges. Call this magical black box thingy your solver. How long this solver takes and what it does inside the black box is not a concern. It just always gives you the right answer.

An explicit steady solver is the for-the-most-part the same as an explicit transient solver. The idea is to keep advancing the solution in time until the time-derivative vanishes. Explicit steady solvers try to use really large time-steps (acceleration) to speed this up. But with every advance in time, you have a new solution state and this gets shown to the user often as an iteration.

With implicit solvers you also have a current solution state. You have a system of equations that needs to be solved for the next time-step which you feed through your black box solver and it returns an updated solution. Here you also advance the solution in time but since there's no real concept of time in a steady state problem, the user interprets this as an iteration.

What's invisible is what is this magical time-step and what temporal discretization has been used? They don't seem to be an input anywhere... I just click a button that says steady state... Since I didn't choose any temporal discretization and didn't choose a time-step, that means there isn't any right....? It's hidden inside the black box!


This is one of the reasons why you have to provide an initial guess even for steady state solvers. If there was a more powerful black box solver that could solve the steady equation, you wouldn't need to provide an initial guess. It would just be able to tell you the steady state solution without any inputs other than the governing equation and boundary conditions.

[FMDenaro]

For steady equations there are no implicit/explicit time integration.
However, the explicit and implicit denomination makes sense in the FD discretization in some cases of spatial discretization. For example we use explicit FD formula based on Taylor expansion as well as implicit FD when compact scheme are used.

[granzer]

@LuckyTran

Originally Posted by LuckyTran

An explicit steady solver is the for-the-most-part the same as an explicit transient solver. The idea is to keep advancing the solution in time until the time-derivative vanishes. Explicit steady solvers try to use really large time-steps (acceleration) to speed this up. But with every advance in time, you have a new solution state and this gets shown to the user often as an iteration.

Considering steady state heat equation, how to "keep advancing in time" as there is no time term? i.e
When considering the steady state heat equation the transient derivative term is taken to be zero. When discretizing the SS heat equation there are no current and future time step. If we say that (for the transient heat equation), the temperature at the next time step is given interms of the the temperature at current time step (known values) is called explicit discetization and that the temperature at the next time step is given interms of the the temperature at current time step(known) and the next time step (unknown values) is called implicit discetization THEN what is the known and unknown terms when considering steady state heat equation (as there is no concept of current and next time step)?

[FMDenaro]

Originally Posted by granzer

@LuckyTran
Considering steady state heat equation, how to "keep advancing in time" as there is no time term? i.e
When considering the steady state heat equation the transient derivative term is taken to be zero. When discretizing the SS heat equation there are no current and future time step. If we say that (for the transient heat equation), the temperature at the next time step is given interms of the the temperature at current time step (known values) is called explicit discetization and that the temperature at the next time step is given interms of the the temperature at current time step(known) and the next time step (unknown values) is called implicit discetization THEN what is the known and unknown terms when considering steady state heat equation (as there is no concept of current and next time step)?

Simple heat equation in strady, 1D, linear case


u*dT/dx-alpha*d^2T/dx^2=0


this is valid at any time, you introduce a FD discretization and will see that the linear algebric system A*x=0 (+BCs) is obtained.
There is no old and new state vector, you just solve the system. No explicit or implicit method exists.

[LuckyTran]

There are true steady state solvers where there is no concept of time. Question is whether you have a true steady solver or whether you have a transient solver in disguise.

Originally Posted by granzer

@LuckyTran
Considering steady state heat equation, how to "keep advancing in time" as there is no time term? i.e
When considering the steady state heat equation the transient derivative term is taken to be zero. When discretizing the SS heat equation there are no current and future time step. If we say that (for the transient heat equation), the temperature at the next time step is given interms of the the temperature at current time step (known values) is called explicit discetization and that the temperature at the next time step is given interms of the the temperature at current time step(known) and the next time step (unknown values) is called implicit discetization THEN what is the known and unknown terms when considering steady state heat equation (as there is no concept of current and next time step)?

Even if there isn't an explicit time parameter, there can be one implicitly. Here, explicit/implicit refers to something else than discretization. In other words, the solution has changed from one-step to the next, and this is analogous to a change in time (hence implicit time). The solution at each step is a at a time (the wonky implicit time variable, not the explicit one that you associate with the clock). The current time is analogous to current step and next time is analogous to the next step.

If your solver wasn't a black box, you would know (or at least be able to find out) the explicit coefficient matrix and/or the implicit linear system describing this evolution.

If you have a a transient solver in disguise, then there is a concept of implicit/explicit time-stepping even when there isn't an explicit time parameter but an implicit time parameter.

To pose a hypothetical question: if I were to give you two solutions at two times, it can be explicit or implicit time-stepping, would you be able to figure out what the time-step size was?


Bottom line is, you have the right to be confused when no one is telling you how the steady state problem is being solved in the first place. Or what even is the steady state problem.

[granzer]

Originally Posted by FMDenaro

Simple heat equation in strady, 1D, linear case


u*dT/dx-alpha*d^2T/dx^2=0


this is valid at any time, you introduce a FD discretization and will see that the linear algebric system A*x=0 (+BCs) is obtained.
There is no old and new state vector, you just solve the system. No explicit or implicit method exists.

But since we do get a system of equation (ie the required terms/variable at a point in space given in terms of other points in space(which may be know, like BC, or unknown)) wont it be a implicit scheme then?

[LuckyTran]

Originally Posted by granzer

But since we do get a system of equation (ie the required terms/variable at a point in space given in terms of other points in space(which may be know, like BC, or unknown)) wont it be a implicit scheme then?

No, you get a system like 3x=6. The solution is just 2.

If you actually do carry out the discretization for the simple heat equation with constant material properties etc. (this is a good exercise to do!), you will find that (for the Ax=b system) A is a simple matrix of known numbers. A will not contain any x's in it.


For the not-so-simple equation with non-linearities, variable material properties and such, A will then depend on x.

[granzer]

Originally Posted by LuckyTran

No, you get a system like 3x=6. The solution is just 2.

If you actually do carry out the discretization for the simple heat equation with constant material properties etc. (this is a good exercise to do!), you will find that (for the Ax=b system) A is a simple matrix of known numbers. A will not contain any x's in it.


For the not-so-simple equation with non-linearities, variable material properties and such, A will then depend on x.

Originally Posted by FMDenaro

Simple heat equation in strady, 1D, linear case


u*dT/dx-alpha*d^2T/dx^2=0


this is valid at any time, you introduce a FD discretization and will see that the linear algebric system A*x=0 (+BCs) is obtained.
There is no old and new state vector, you just solve the system. No explicit or implicit method exists.

Thank you @LuckyTran and @FMDenaro, I think i am beginning understand it the terminology.
Just to make sure my understanding is correct what would be the when solving for Laplace equation? would there be a implicit/explicit time involved to give the solution (so implicit or explicit discretization form) ? and what would be the case if time is not involved (that what I think you meant by true steady state sovler right @LuckyTran?) is there a implicit and explicit form of solution then too?

[FMDenaro]

Originally Posted by granzer

Thank you @LuckyTran and @FMDenaro, I think i am beginning understand it the terminology.
Just to make sure my understanding is correct what would be the when solving for Laplace equation? would there be a implicit/explicit time involved to give the solution (so implicit or explicit discretization form) ? and what would be the case if time is not involved (that what I think you meant by true steady state sovler right @LuckyTran?) is there a implicit and explicit form of solution then too?

Time can be involved in paraboli and hyperbolic equations. Laplace equation is elliptic, it states a solution in equilibrium that is valid for any time.
Again, implicit/explicit FD can be somehow used also when time is not present but it addresses the way in which the finite derivative are explicitly or implicitly computed. That is totally different from the explicit/implicit time-marching schemes

[granzer]

Originally Posted by FMDenaro

Time can be involved in paraboli and hyperbolic equations. Laplace equation is elliptic, it states a solution in equilibrium that is valid for any time.
Again, implicit/explicit FD can be somehow used also when time is not present but it addresses the way in which the finite derivative are explicitly or implicitly computed. That is totally different from the explicit/implicit time-marching schemes

@FMDenaro Exactly! when I was talking about the steady-state heat equation I meant the heat equation reduced to Laplace equation (at the steady state condition.) Can you please elaborate on how it can be implicit explicit FD method can be used here. All the reference materials I have studied always talk about implicit and explicit FD schemes as if they can be applied to all the problems as if they can be applied to all the problems but only explain it with examples of parabolic and hyperbolic equations. Since elliptic equations take information from all around a given point how can it be given in implicit and explicit forms? I couldn't find any material which talks about implicit/explicit schemes applied to elliptic equations. Can you please suggest any study material here this is explained.

[FMDenaro]

Originally Posted by granzer

@FMDenaro Exactly! when I was talking about the steady-state heat equation I meant the heat equation reduced to Laplace equation (at the steady state condition.) Can you please elaborate on how it can be implicit explicit FD method can be used here. All the reference materials I have studied always talk about implicit and explicit FD schemes as if they can be applied to all the problems as if they can be applied to all the problems but only explain it with examples of parabolic and hyperbolic equations. Since elliptic equations take information from all around a given point how can it be given in implicit and explicit forms? I couldn't find any material which talks about implicit/explicit schemes applied to elliptic equations. Can you please suggest any study material here this is explained.

You have to distinguish between time-marching explicit/implicit methods (only parabolic and hyperbolic PDE) and explicit/implicit FD formulas for the derivatives. The latter are Padé-based approximations that you find in literature denoted as "compact finite difference" since they use a stencil having a lesser number of nodes than the explicit lagrangian scheme.
Have a look to this paper
https://www.sciencedirect.com/scienc...24R?via%3Dihub

[LuckyTran]

I am worried you have utterly confused yourself by attempting to understand a transient problem and transient solver without fully grasping the more basic steady problem and steady solver first.

Laplace's equation gives you a matrix system 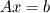. And you can solve this just like you solve a linear system. An inefficient but analytical way of showing how to do this is find the inverse of A and multiply both sides by this inverse. 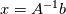. This is your heavenly black box. So now think of why you need an iterative solver to solve Laplace's equation... I'm now going to switch to an example of one equation.

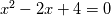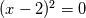If you solve the system analytically, the solution is just 2 because . Here there is no concept of time and the solution is 2 all-the-time.

Solving this same problem using a different method gives you a bunch of things to think about. You can also solve this problem using a root finding method like Newton-Raphson method, now you introduce derivatives (and finite differencing is one way to approximate them) and you have options of when to do these (at the initial or final iteration) and this is how implicit/explicit stuff can get involved that have nothing to do really with explicit/implicit time-stepping. Note that the solution to the problem is always 2 no matter what. But Newton's method (the algorithm) is not a method that magically spits out the true solution 2, but steers the initial guess toward something (sometimes towards the solution, sometimes away from the solution). And there is a certain speed at which this guess proceeds towards the solution

Yet another iterative method (but does not involve implicit/explicit business) is to use the bisection method.

[granzer]

Originally Posted by LuckyTran

now you introduce derivatives (and finite differencing is one way to approximate them) and you have options of when to do these (at the initial or final iteration) and this is how implicit/explicit stuff can get involved that have nothing to do really with explicit/implicit time-stepping. Note that the solution to the problem is always 2 no matter what. But Newton's method (the algorithm) is not a method that magically spits out the true solution 2, but steers the initial guess toward something (sometimes towards the solution, sometimes away from the solution). And there is a certain speed at which this guess proceeds towards the solution

Yet another iterative method (but does not involve implicit/explicit business) is to use the bisection method.

@LuckyTran thank you for your patience. I am trying to study the concepts on my own but certain terminologies re confusing. What do you mean by "you have the options of when to do these?" when to do what at the initial or final iteration?

[LuckyTran]

Originally Posted by granzer

What do you mean by "you have the options of when to do these?" when to do what at the initial or final iteration?

In Newton's method (or family of methods that look as such), you need a derivative. You have at least three choices. You can take the derivative at the solution (at x=2). In general this doesn't work because you don't know the solution. Or you can take an approximation and get the derivative at the current iteration, this is the explicit approach. Or you can take the derivative at the next iteration, the implicit approach. Doesn't this sound just like a transient solver and explicit/implicit time-stepping? It should. But it's not. It has nothing to do with time, but it is an implicit/explicit approach for getting the spatial derivative.

Note that even if you take the explicit derivative, you still have to do many iterations before you can find the right root.

It is the exact same steady problem but depending on how you choose to solve it, there can be no concept of time and no confusion about what is explicit or implicit. Or there can be! So when you say I have a steady solver... you need to tell us what is your steady solver!