 |
|
|
[Sponsors] | |||||
Number of equation by using eddy viscosity turbulence models |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
Hello,
i'm trying to understand the theory behind the eddy viscosity turbulence modelling. First i'm doing the RANS approach on the conservation equations and i get the Reynolds Stress tensor like in the picture (Reynold_Stress_Tensor) below. Each line characterize the additonal terms that i get in the three momentum equation. By choosing a eddy viscosity turbulence model, i use the approach of Boussinesq for modelling the expressions of the Reynolds Stress Tensor. There is an unknown variable, the turbulent viscosity. The definition of the turbulent viscosity depends on the choosen turbulence model. Let's choose the k-epsilon model for example. https://www.cfd-online.com/Wiki/Stan...-epsilon_model In the equations of k and epsilon, you can find the indices i and j which go from 1 to 3 each (direction x,y,z). If i=1, j could be 1,2,3, so i have 3 equations in total for k in x-direction ? All in all i have 9 equations for k and 9 equations for epsilon? Than i have lots of opportunities to calculate the turbulent viscosity and the entries of the Reynolds Stress Tensor. Or do i have just 9 additonal equations (one for each entrie of the Reynolds Stress Tensor). For example i want to calculate the first entry. Than, i and j are 1 and it "goes down" to the equation of the turbulence model? So the main question is, how many equations do i get in total. I hope that i describe my problem in a good way. It would be great if someone could explain it to me. Thanks a lot, bumper |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,681
Rep Power: 66    |
You get 3 scalar momentum equations because it's a 3-dim vector. Really you could equivalently say you have 1 momentum equation.
You get 1 equation for k and 1 equation for epsilon because they're both scalars. The fact that you see an i,j, or k in the k and epsilon equations doesn't really mean you get 3 new equations each. If you write out the entire equations, you'll find there is just 1 equation each. You have to follow the summation rules for the notation being used. Even though the Stress Tensor has 9 entries in the matrix, you still get 3 momentum equations. You have to pay attention to the products of vectors and tensors. What you need to get the turbulent viscosity is k and epsilon. Once the turbulent viscosity is known, you get all the components of the reynolds stress tensor from the boussinesq hypothesis. You get k and epsilon by solving their transport equations, respectively. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
Okay, i have three momentum equations, that's clear. 3 entries (one line) of the Reynolds Stress Tensor belong to one momentum equation.
So the i,j or k in the equation for the energy or dissipation doesn"t mean, that i get a 3dimensional equation. There is only one equation for the energy k and one for the dissipation rate. Which summation rules do you mean? I see just a partial derivation. That's the reason why i was expacting 3 equation each. Can you show me how the entire equation looks like? Thanks a lot for your help. |
|
|
|

|
|
|
|
|
#4 | |
|
Member
E
Join Date: Mar 2018
Posts: 77
Rep Power: 8  |
Quote:
Can you suggest a book with numerical schemes solving k and epsilon equations? Many of CFD books describe for example SIMPLE, SIMPLER, PISO etc algorithms but do not mention numerical methods for solving for example k-epsilon equations. |
||
|
|

|
||
|
|
|
#5 | ||
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,681
Rep Power: 66    |
Quote:
As an example, the momentum equations look like this when you expand all the summations. Yes this is the navier-stokes & not the RANS. The stress tensor and reynolds stress tensor are similar anyway and the difference is mainly in the effective viscosity. Despite there being 9 combinations of indices, you get only an x,y,z equations. There's no magic here, you just have to follow the rules for the notation being used. Quote:
Other equations like energy, k, epsilon, etc. don't have this issue. All you need is some type of linear solver (i.e. solve Ax=b). You just need a way to solve this linear system. The dumb way is to invert A. Gauss-Seidel algorithm is another archetype. Even when you execute the SIMPLE algorithm, you will use similar solvers to solve the individual pieces of the SIMPLE algorithm because the first step in SIMPLE is to solve the momentum equation with an assumed pressure field. |
|||
|
|

|
|||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,782
Rep Power: 71    |
I think that a brief observation is required in case of incompressible flows.
The eddy viscosity model is written for the deviatoric part of the tensor, the isotropic part (the trace) being incorporated into the "pressure". From that you can write the three scalar equations |
|
|
|

|
|
|
|
|
#7 | |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
Quote:
Thanks for your help. |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,782
Rep Power: 71    |
I am not sure to understand the key of these doubts...In the eddy viscosity model, you substitute the full unknown tensor with the modelled tensor. One does not pretend to substitute each entry of the Reynolds tensor with a modelled entry.
At the end you have a term like this: Div(2*mu_total*S) being S the symmetric part of the velocity gradient with zero trace. Now, to get the contribution to one of the scalar momentum equations, just project the term along a direction ei Last edited by FMDenaro; August 1, 2019 at 06:46. |
|
|
|

|
|
|
|
|
#9 | |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
Quote:
Expressions in equation for x mometum: First line Expressions in equation for y mometum: Second line And so on... |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,782
Rep Power: 71    |
Quote:
So, you are not interested to the eddy viscosity modelling but only on the unresolved Reynolds stress? In such case just consider that this tensor is nothing but as same as you have in the classical convective term Div (vv). Along the x-direction you write i.Div (v'v'), along y j.Div (v'v') and so on (I did not write the averaging). for example, the x component: d/dx(u'u')+d/dy(v'u')+d/dz(w'u') |
||
|
|

|
||
|
|
|
#11 |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
Sure, i"m interested to the eddy viscosity modelling but i want to understand the Reynolds Stress tensor and the equations behind.
If the tensor is nothing but as same as you have in the classical convective term Div, i'm right with the lines of the Reynolds stress tensor and the equations of momentum, right? |
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,782
Rep Power: 71    |
Quote:
yes, the expression I wrote above is the same in the figure you posted |
||
|
|

|
||
|
|
|
#13 |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
To sum it up and to check if i unstand it in the right way, the Reynolds Stress Tensor is the summary of additonal entries which i get through the Reynolds-approach in the equations of momentum right?
|
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,782
Rep Power: 71    |
Quote:
yes, is exactly as same expression as when you write the convective terms, that is d/dxi(u'i u'j). |
||
|
|

|
||
|
|
|
#15 |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
Perfect, than thanks a lot for your help
|
|
|
|

|
|
|
|
|
#16 | |
|
Member
E
Join Date: Mar 2018
Posts: 77
Rep Power: 8  |
Quote:
Thank you. So lets take the k equation in k-epsilon model. Can we discretize this equation with standard schemes applied for convective-diffusive terms like ADI and solve it for example with Gauss-Seidel or Jacobi? |
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,681
Rep Power: 66    |
Quote:
Yes. Usually in CFD the advection terms are the trouble maker in terms of accuracy and stability, but specifically the advection term in the momentum equation (it's non-linear) is where all the attention goes. The advection terms in k and epsilon equations are linear with respect to k and epsilon and much easier to solve and give much fewer headaches. That's why we don't really talk about them much. If you can solve the much tougher momentum equation, the rest are easier. |
||
|
|

|
||
|
|
|
#18 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,782
Rep Power: 71    |
Quote:
Well, actually there is a problem in the transport of k as it is assumed to be a non-negative variable and a monotonicity-preserving scheme should be properly used. |
||
|
|

|
||
|
|
|
#19 | |
|
Member
E
Join Date: Mar 2018
Posts: 77
Rep Power: 8  |
Quote:
Thank you. |
||
|
|

|
||
|
|
|
#20 |
|
New Member
Join Date: May 2019
Posts: 18
Rep Power: 7  |
I have an additional question about the turbulence modelling. For the calculation of the turbulent viscosity, you're going to solve differential equations for k and epsilon.
I found additional euqations for k and epsilon. 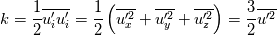 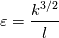 During the simulation, i think the differential euqations will be used for k and epsilon. But when and for what usage are the named equations for k and epsilon? |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Foam::error::PrintStack | almir | OpenFOAM Running, Solving & CFD | 92 | May 21, 2024 07:56 |
| Setting the height of the stream in the free channel | kevinmccartin | CFX | 12 | October 13, 2022 21:43 |
| Problem with divergence | TDK | FLUENT | 13 | December 14, 2018 06:00 |
| [mesh manipulation] Mesh Refinement | Luiz Eduardo Bittencourt Sampaio (Sampaio) | OpenFOAM Meshing & Mesh Conversion | 42 | January 8, 2017 12:55 |
| Unaligned accesses on IA64 | andre | OpenFOAM | 5 | June 23, 2008 10:37 |